第一章． 函数

变量。

在函数的概念之前，首先人们从对事物的变化发展的观察中，抽象出来变量的概念，在数学的历史上，正是变量的出现导致代数学的发展。因为在没有变量概念的时候，人们进行算术运算，只会做到对具体的数值进行运算。每次遇到稍微不同一些的数值，都必须很费劲地重新考虑计算方法，只有在抽象出来变量的概念后，才能对一般的数值计算抽象出来一般的计算方法，从而彻底地解决数值地计算问题。而代数学正是为了发展一般的数值计算方法而发展起来的。因此可以说变量概念的出现是数学发展历史上的第一个里程碑。

函数。

自然界里的观察量都可以看成是变量，然后我们从自然界里归纳出的自然规律常常表现为变量与变量之间的依赖关系。而函数实际上就是为了表述这些变量与变量之间的依赖关系而抽象出来的数学观念。

我们常常把相互之间具有依赖关系的一些变量区分为两类，一类被称为自变量，一类被称为因变量。因此这个依赖关系就可以理解为因变量如何被自变量决定的关系。

函数从一般的依赖关系中抽象出三个要素作为函数的基本要素。首先就是依赖关系本身，也即一个或几个变量（自变量）是如何决定另一个变量（因变量）的，这种决定关系还必须是唯一的，因为我们研究的这种依赖关系总是一种具有确定性的关系。也就是说，从一些自变量的数值，能够唯一地得到另一个因变量的数值。这是函数概念里的一个关键所在。也是初学者常常犯错误的地方。

要表示一种依赖关系，可以有很多的方式。

最直截了当的就是一一列出变量之间的所对应的数值。例如我们常用的数学用表，列车时刻表，税单，等第，这种表示方法的好处就是一目了然，能让你很快的查到你所需要的变量的值，甚至是精确的值，而无须进行另外的计算，缺点就是只能处理很有限的数值，对于可以取大量，甚至无穷的数值的变量，这种方法就不行了。另外还不能容易地让人理解变量之间地对应规律。

要想能容易地让人理解变量之间的对应规律，可以使用图示的方式。

对于一元函数y=f（x），它的变量相应地在平面上的直角坐标系的X轴和Y轴上取值，在一定条件下，就能得一个几何图象，表达了函数的数值分布。用图来表示变量之间的依赖关系，可以很直观地说明这种依赖关系的很多性质。在高等数学的学习中，我们也应该善于通过画图来培养对于抽象概念的直观能力，而初学者往往忽略这点，甚至不屑于此，这是我们应该极力避免的。图示的缺点就是不能精确地给出数值，也不能精确地表达函数的性质。

最精确的表达方式是给出函数关系的解析表达式。有了解析表达式，就可以对已知数值进行确定的数学计算，从而得到未知量的精确数值。更进一步，通过对解析表达式的数学分析，可以得到函数性质的精确的表达。而我们学习微积分的主要目的，就是掌握这种分析方法。

当然还可以有其他的表示函数的依赖关系的方法，总之只要能说明一个变量如何由另外的变量唯一决定就行。

表示了依赖关系之后，还必须说明其中自变量的取值范围。因为在实际问题中，有时候并不能从依赖关系本身就得到自变量的取值范围。因此还必须单独规定。这个取值范围被称为定义域。

有了自变量的取值范围，加上函数的对应关系，就可以得到因变量的取值范围，这就是函数的第三个要素，被称为值域。

总结一下，函数概念最关键的地方，就是它的对应关系，或者说依赖关系，必须是因变量由自变量唯一确定。尽管我们可以考虑一对多的多值函数，比方说解析几何里的一些曲线方程，要对它们应用微积分的方法，那种情形必须给予特别的处理，或者把它们分割为多个函数，总之为了统一地发展我们后面要讨论地微积分技术，我们总是坚持这一点为函数的必要条件。

第二点需要特别用心的地方就是根据函数关系由定义域求值域。或者是只是根据函数关系的数学表达式本身，来求出具有数学意义的定义域和值域，或者还要求具有实际意义而不只是具有数学意义的定义域和值域。这就要求我们熟练掌握各种函数的数学性质，特别是我们下面要讨论的几种基本初等函数的性质。我们将在下面结合例题更详细地讨论这点，并且希望读者多作练习。

并不是说我们需要把一个函数用某种方式给出，就可以说是已经掌握了这个函数。因为对于一个函数的了解，并不是知道了这个函数所代表的所有数值对应，就能判断这个函数的行为与性质，在实际问题当中，我们更加需要得到的是一个函数的性质，因为某种变化规律所具有的性质，往往表达了某个概念，而我们人类对于事物的了解最终是基于概念的理解，而不是一堆数据本身。

下面我们就来讨论函数所可能具有的几种性质。这几种性质都具有非常直观的意义，只需要用初等的方式就可以表达出来。

（一）函数的单调性。

从直观的感觉来看，所谓单调表明了函数在某点附近具有平滑的变化，如果把函数的自变量与因变量分别在平面上的直角坐标系的两个坐标轴上取值，得到函数的图象，就可以看到函数在某点附近的单调性，意味着函数在这点附近没有剧烈的震荡，或者这点左边的点的函数值比右边的点的函数值大，或者反过来右边的点的函数值比左边的点的函数值大。这样在一个区间内每个点都具有同样的一个性质，就可以定义这个区间的单调性。

精确地说，函数y=f（x）在区间K内的任意两点a，b，只要a<b,就有f(a)<f(b).或者是f(a)>f(b).那么就称这个函数在区间K具有单调性，如果是f(a)<f(b)的情形，则称为单调增加,如果是f(a)>f(b)的情形，则称为是单调减少。这是严格的情形，如果上面的大于和小于分别是大于或等于和小于或等于，则是非严格的单调性。

注意上面定义里的任意两个字，应该说这是一个很严格的条件。也是单调性定义里的关键所在。

设想一下，如果我们有一个函数，完全由所有的数值的对应来表达，那么要判断这个函数在一个区间内的单调性，则需要对这个区间内的所有数值顺序进行比较，显然，如果是对于一般的函数，这是非常困难的事。不过如果是用我们常见的一般的解析表达式给出的函数，通过直接对解析表达式进行比较，则是非常容易判断的。这里的关键是我们常见的一般的解析表达式给出的是变化比较平滑的函数，而如果函数的图象如下所示，则只有在极其小的区间内才有可能考虑函数的单调性。

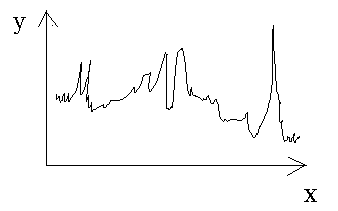
（二）函数的有界性；

从直观的感觉来看，函数的有界性就是函数图形在某个特定范围或者是在整个定义域的上下“高度”有限。或者就说是函数在某个特定区间或者在整个定义域都不存在函数取值为正无穷大或负无穷大的点。

精确地说，就是取函数f（x）有定义的一个集合K，如果存在一个确定的正数M，无论M可能有多么大，只要对于集合K内的所有的点x，都有成立，那么就称函数f（x）在集合K上有界。

注意上面定义中函数外面的绝对值符号，这表明有界性是同时在上下加以限制的。

这个性质是非常好理解的。之所以提出这么一个性质出来，倒不是因为有界性具有什么特别的趣味，而是反过来，不具有有界性的函数常常是我们必须加以注意和分析的对象，因此我们提出函数的有界性，正是为了用于判断函数是否存在无界的性质。

从上面的定义可以看到，我们是无法直接应用这个定义来证明某个函数是否有界的，因为这是一个存在性定义，我们必须通过其他的方法，来找到这么一个M，才能得到证明，而如何找到这个M，则是这个定义所没有给出的。

另外，对于这个M，只是要求其存在性，而没有要求其唯一性，实际上，这个M不可能具备唯一性，因为只要存在一个M满足条件，由于M是一个有限大小的正数，那么任何一个比M大的数同样可以作为函数的界。

下面是用图象表示的有界性的两种典型情况：

（三）函数的奇偶性；

同样可以从图象方面得到对于奇偶性的很好的理解，就是看在某个区间内，整个函数图形是否具有对于Y轴的镜象对称或者对于原点的中心对称性。这样我们至少可以知道，首先这个函数的定义域必须是X轴上关于原点对称的。

精确地说，就是取函数有定义的一个关于原点对称的区间（-L，L），

（1） 如果对于在区间（-L，L）内任意的一点x，都有f（-x）=-f（x），那么f（x）就是这个区间内的奇函数。

（2） 如果对于在区间（-L，L）内任意的一点x，都有f（-x）=f（x），那么f（x）就是这个区间内的偶函数。

我们可以看到，这个定义是与有界性的定义不同的一种定义方式，就是我们一般可以直接应用这个定义来证明某个函数的奇偶性，这种定义方式就是属于构造性的定义方式。也就是直接给出了符合定义的对于如何构造出来。在今后的学习当中，我们应该注意到这两种定义方式的差别所在。

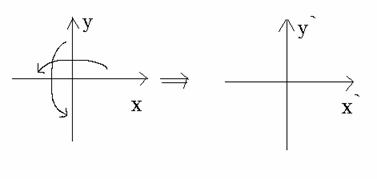
这里我们还应该体会到在坐标系里，对函数进行反射变化实际上就是进行如下变量代换：

关于原点的中心对称变换：

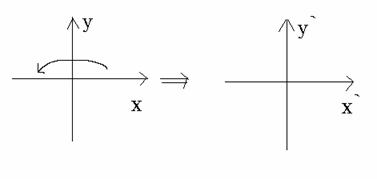
关于Y轴的镜面反射变换：

而如果在这样的变换之下，函数的形式并没有变化，那么对于关于原点的中心对称变换，就是奇函数；对于Y轴的镜面反射变换，就是偶函数。

那么我们在证明某个函数是否具有奇偶性，或者是奇函数还是偶函数，就可以直接应用这个变量变换，从而得到判据。

（四）函数的周期性。

从直观上来看，就是整个函数图形是否可以通过沿着X轴，无论是朝哪个方向，平移一个有限大小的距离，得到的函数图象与原来的函数图象可以完全重合。也就是说具有沿着X轴的平移不变性质。把这个意思精确表达出来，就是周期性的定义：

对于实数上定义的函数y=f（x），如果存在一个非零的实数a，使得

f（x）=f（x+a）

总是成立，那么就说函数y=f（x）是实数上的周期函数，周期为a。

注意，这里a的正负无所谓，因为函数在整个X轴上定义，a为正数，只是表明函数沿着X轴向右平移a的距离，a为负数，只是表明函数沿着X轴向左平移a的距离，这两种平移方式是等价的。

可以看到，严格的平移不变性要求函数在整个X轴上都有定义，否则，进行平移必定会使得函数超出本来的定义域。不过，在某些情况下，也可以定义在有限区间内的周期性，只是这时候就不能应用这个定义了，而只能具体地规定函数有限的周期性。一般我们不考虑这样的函数。

在周期性的定义里，我们还可以看到，这个定义也是属于存在性定义，也就是说，直接从定义出发，我们无法得到具体的周期，尽管要证明一个函数的周期性，并不一定需要求出具体的周期a是多少，但无论如何，我们必须从别的地方入手来证明周期的存在性。

周期函数的一个特例是y=a，其中a是一个常数。这个函数的周期是任意的实数。

函数的反函数。

我们从函数的定义可以很自然地得到非常有意义的反函数的概念。

所谓函数无非就是自变量与因变量的数值对应，因此这种对应也可以在相反的方向上成立，即因变量的数值与自变量的数值的对应。当然，如果要想使得得到的这个新的数值对应仍然还是一个函数，就必须还满足一个条件，就是因变量的每一个数值，对应于唯一的一个自变量的数值，再把这个条件和本来的要求自变量的每一个数值，对应于因变量的唯一一个数值加起来，就得到了一个函数存在反函数的充要条件是：自变量和因变量必须一一对应。

现在我们就可以形式地表达反函数的概念如下：

对于一个函数y=f（x），如果对于每一个因变量y的值，只存在唯一的一个自变量的值和它对应，那么可以把这种从因变量到自变量的关系看成一个新的函数：x=g（y）。这个新的函数就是函数y=f（x）的反函数。

从直观上来看，就是把一个函数对直线x=y进行镜象反射所得到的函数。

注意：初学者常常在这里产生很多混乱的印象。

首先相互作为反函数的两个函数，实际上是对具有一一对应关系的两个数值集合之间所存在的关系的两种看法，也就是说，是两种不同的对应关系，而不能认为是同一个对应关系。

因此y=f（x）的反函数不能写成x=f（y），函数符号f（），表示一个特定的对应关系，那么y=f（x）与x=f（y）就只是对应关系相同，此外是完全没有任何关系的两个函数。如下图所示：

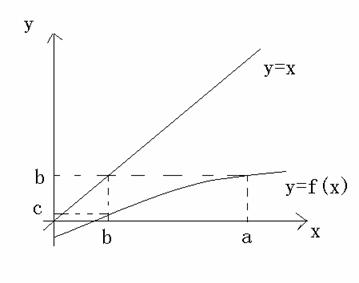
如果我们在函数y=f（x）上取一点（a，b），即有b=f（a），如果再取x=b，则得到c=f（b），我们可以看到（a，b）和（b，c）这两点，并非关于直线y=x对称，也就是说，a不等于c，即当a通过一个函数关系对应于b时，b通过相应的反函数关系并不是对应于a，要使得在这种情况下，有a=c，只有唯一的函数y=x满足这个条件。

下面我们开始讨论具体的函数，它们是我们在这门课程里最主要的研究对象。也是我们进一步研究更复杂的函数的基础，尽管读者可能已经在高中阶段学习过这些函数，但仍然需要用更深刻的观念来把握它们的具体性质。鉴于它们的重要性，我们必须仔细地学习它们，下面分别地根据图形进行分析。

初等函数。

所谓初等函数并非一个很严谨的概念，一般说来，就是指以下五种基本初等函数，以及通过对这五种初等函数进行有限运算与有限复合而得到的任意函数。这只是从一般的构成方法来说的，并非从应该具备什么样的限制这方面来说的。

下面我们从构成初等函数的基本组成部分开始讨论。

（1）幂函数；

幂函数的一般形式为。

如果a取非零的有理数是比较容易理解的，不过初学者对于a取非零的无理数，则不太容易理解，在我们的课程里，不要求掌握如何理解指数为无理数的问题，因为这涉及到实数连续统的极为深刻的知识。因此我们只要接受它作为一个已知事实即可。

对于a的取值为非零有理数，有必要分成几种情况来讨论各自的特性：

首先我们知道如果，q和p都是整数，则，而如果，则，因此可以看到x所受到的限制来源于两点，一是有可能作为分母而不能是0，一是有可能在偶数次的根号下而不能为负数，那么我们就可以知道：

排除了为0与负数两种可能，即对于x>0，则a可以是任意实数；

排除了为0这种可能，即对于x<0和x>0的所有实数，p不能是偶数；

排除了为负数这种可能，即对于x为大于且等于0的所有实数，a就不能是负数。

总结起来，就可以得到当a为不同的数值时，幂函数的定义域的不同情况如下：

如果a为任意实数，则函数的定义域为大于0的所有实数；

如果a为负数，则x肯定不能为0，不过这时函数的定义域还必须根据p的奇偶性来确定，即如果同时p为偶数，则x不能小于0，这时函数的定义域为大于0的所有实数；如果同时p为奇数，则函数的定义域为不等于0 的所有实数。

在x大于0时，函数的值域总是大于0的实数。

在x小于0时，则只有同时p为奇数，函数的值域为非零的实数。

而只有a为正数，0才进入函数的值域。

由于x大于0是对a的任意取值都有意义的，因此下面给出幂函数在第一象限的各自情况.

可以看到：

（1）所有的图形都通过（1，1）这点。

（2）当a大于0时，幂函数为单调递增的，而a小于0时，幂函数为单调递减函数。

（3）当a大于1时，幂函数图形下凹；当a小于1大于0时，幂函数图形上凸。

（4）当a小于0时，a越小，图形倾斜程度越大。

（5）a大于0，函数过（0，0）；a小于0，函数不过（0，0）点。

（6）显然幂函数无界。

（2）指数函数；

指数函数的一般形式为，从上面我们对于幂函数的讨论就可以知道，要想使得x能够取整个实数集合为定义域，则只有使得

如图所示为a的不同大小影响函数图形的情况。

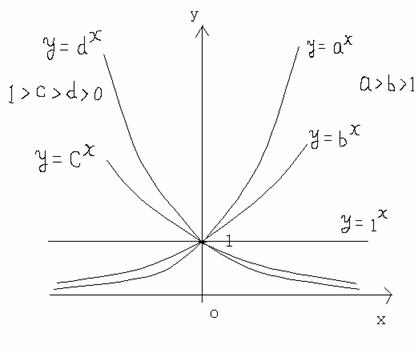
可以看到：

（1） 指数函数的定义域为所有实数的集合，这里的前提是a大于0，对于a不大于0的情况，则必然使得函数的定义域不存在连续的区间，因此我们不予考虑。

（2） 指数函数的值域为大于0的实数集合。

（3） 函数图形都是下凹的。

（4） a大于1，则指数函数单调递增；a小于1大于0，则为单调递减的。

（5） 可以看到一个显然的规律，就是当a从0趋向于无穷大的过程中（当然不能等于0），函数的曲线从分别接近于Y轴与X轴的正半轴的单调递减函数的位置，趋向分别接近于Y轴的正半轴与X轴的负半轴的单调递增函数的位置。其中水平直线y=1是从递减到递增的一个过渡位置。

（6） 函数总是在某一个方向上无限趋向于X轴。

（7） 函数总是通过（0，1）这点。

（8） 显然指数函数无界。

（3）对数函数；

对数函数的一般形式为，它实际上就是指数函数的反函数。因此指数函数里对于a的规定，同样适用于对数函数。

下图给出对于不同大小a所表示的函数图形：

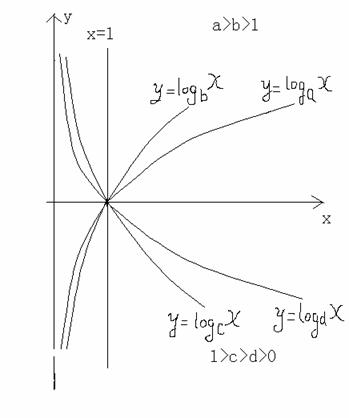
可以看到对数函数的图形只不过的指数函数的图形的关于直线y=x的对称图形，因为它们互为反函数。

（1） 对数函数的定义域为大于0的实数集合。

（2） 对数函数的值域为全部实数集合。

（3） 函数总是通过（1，0）这点。

（4） a大于1时，为单调递增函数，并且上凸；a小于1大于0时，函数为单调递减函数，并且下凹。

（5） 显然对数函数无界。

（4）三角函数；

三角函数分成6种形式，都是典型的周期函数：

正弦函数：y=sinx;

余弦函数：y=cosx;

正切函数：y=tgx;

余切函数：y=ctgx;

正割函数：y=secx;

余割函数：y=cscx.

下面分别结合函数的图形来讨论它们的性质。

正弦函数：y=sinx与余弦函数：y=cosx：

下面是正弦函数和余弦函数的图形：

可以看到：

（1） 这两种函数的周期都是。

（2） 余弦函数y=cosx沿着X轴的正方向平移，就与正弦函数y=sinx完全重合。

（3） 它们的定义域都是实数。

（4） 它们的值域都是大于等于-1，小于等于1。

（5） 它们都是有界的。

（6） 正弦函数为奇函数。

（7） 余弦函数为偶函数。

正切函数：y=tgx，余切函数：y=ctgx：

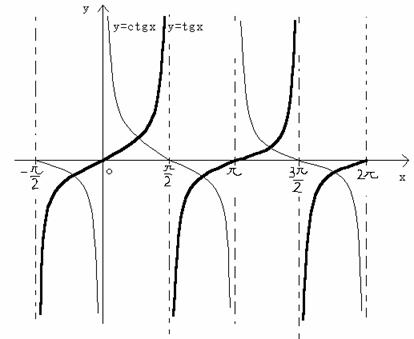
下图中，粗线是正切函数的图形，细线是余切函数的图形，从图形可以看到：

（1） 它们都是周期函数，周期都是。

（2） 正切函数的定义域是实数轴上，除了这些点以外的所有点的集合。

（3） 余切函数的定义域是实数轴上，除了这些点以外的所有点的集合。

（4） 它们的值域都是实数集合。

（5） 在两个间断点之间，正切函数是单调递增函数，而余弦函数是单调递减函数。

（6） 正切函数无限趋向于直线x=。

（7） 余切函数无限趋向于直线x=。

（8） 它们都是无界函数。

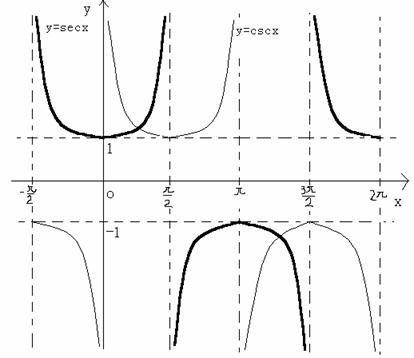
正割函数：y=secx，余割函数：y=cscx：

下面的图中，粗线是正割函数的图形，细线是余割函数的图形。从图可以看到：

（1） 它们都是周期函数，周期都是。

（2） 正割函数的定义域是实数轴上，除了这些点以外的所有点的集合。

（3） 余割函数的定义域是实数轴上，除了这些点以外的所有点的集合。

（4） 它们的值域都是实数集合里大于1和小于-1的实数集合。

（5） 正割函数无限趋向于直线x=。

（6） 余割函数无限趋向于直线x=。

（7） 它们都是无界函数。

（8） 正割函数为偶函数。

（9） 余割函数为奇函数。

（5）反三角函数；

6种三角函数都有相应的反函数，称为反三角函数，它们是：

反正弦函数：y=arcsinx;

反余弦函数：y=arccosx;

反正切函数：y=arctgx;

反余切函数：y=arcctgx;

反正割函数：y=arcsecx;

反余割函数：y=arccscx.

由于6种三角函数都是周期函数，因此从严格的意义上来讲，它们不存在反函数，而只有把它们的定义域进行适当的限制以后，才可以说是存在反函数。反过来，也可以说是对反三角函数的值域进行适当的限制。

对于正弦函数，正切函数，余割函数，要构造相应的反函数，值域一般取为。

对于余弦函数，余切函数，正割函数，要构造相应的反函数，值域一般取为。

这样我们就得到了满足函数定义的反三角函数，下面我们分别结合函数的图形进行讨论。

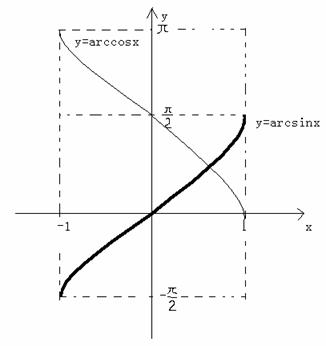
反正弦函数：y=arcsinx，反余弦函数：y=arccosx。

在下图中，粗线为y=arcsinx，细线为y=arccosx。可以看到：

（1） 反正弦函数的定义域为[-1，1]，值域为。

（2） 反余弦函数的定义域为[-1，1]，值域为。

（3） 反正弦函数为单调递增的；反余弦函数为单调递减的。

（4） 它们都是有界的。

（5） 反正弦函数为奇函数。

反正切函数：y=arctgx，反余切函数：y=arcctgx：

在下图中，粗线为y=arctgx，细线为y=arcctgx。可以看到：

（1） 正切函数的定义域为实数集合，值域为。

（2） 反余切函数的定义域为实数集合，值域为。

（3） 反正切函数为单调递增的；反余切函数为单调递减的。

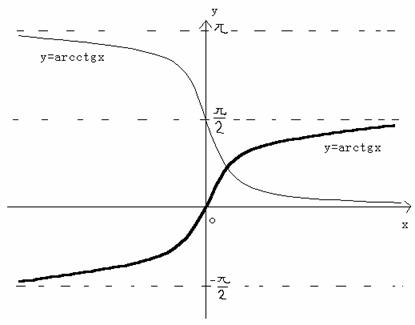
（4） 反正切函数无限趋向于这两条直线。反余切函数无限地趋向于这两条直线。

（5） 它们都是有界的。

（6） 反正切函数为奇函数。

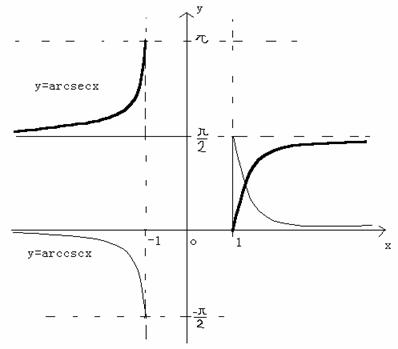
反正割函数：y=arcsecx，反余割函数：y=arccscx：

在下图中，粗线为y=arcsinx，细线为y=arccosx。可以看到：

（1） 正割函数的定义域为，值域为。

（2） 反余割函数的定义域为，值域为。

（3） 反正割函数的两支分别都是为单调递增的；反割弦函数的两支分别都是为单调递减的。

（4） 反正割函数无限趋向于这条直线。反余割函数无限地趋向于这条直线。

（5） 它们都是有界的。

（6） 反余割函数为奇函数。

函数的运算；

我们已经讨论了初等函数的基本类型，对它们进行有限四则算术运算，就可以得到结构更复杂的初等函数，对于这么构成的复杂初等函数，我们仍然有可能根据组成它的基本初等函数的性质来估计它的某些性质，例如在相同的定义域里，两个偶函数的代数和仍然是偶函数，两个有界函数的代数和仍然是有界函数等等，这些都可以根据具体的情况来分析，特别有助于我们在考试时，形成简洁的的解题思路。

函数的复合。

所谓函数的复合，就是进行变量代换。任何一个初等函数z=f（y）的自变量y，如果同时作为另一个函数y=g（x）的因变量，那么把g（x）代入f（y），就得到了一个新的以x为自变量的z的函数z=f（g（x））。这个过程就是函数的复合过程。

在函数的复合过程中，有一个细节需要注意：

g(x)的值域必须是f（x）的定义域的子集；

只有这样才能保证函数复合的合法性。

反过来，我们也可以把一个形式复杂的函数，理解为复合函数，这样就可以按照复合的结构，把它分解为一些形式相对比较简单的形式的函数，从而使得我们能够应用微积分的适当方法对复杂函数进行分析。

另外分析函数的复合结构，也是在分析函数的定义域以及值域时，必须进行的一个步骤，实际上按照函数的复合结构，一步一步地解不等式，正是我们分析复杂函数的定义域以及值域的步骤。

初等函数。

至此为止，我们可以说初等函数的构成，就是把基本初等函数，通过有限次数的四则运算与函数复合而得到的。

这里的关键是有限次数，所谓初等性，其实主要是来自于这个有限性，在后面我们学习无穷级数时，会体会到无穷次数的初等运算不一定可以通过有限的初等函数表示出来。

至于更为确切的初等函数的定义是很难下的，因为在我们的课程里，这个概念本来是一个限制性的概念，并没有非常精确的定义，所以我们也就无须过分地纠缠。

双曲函数和反双曲函数。

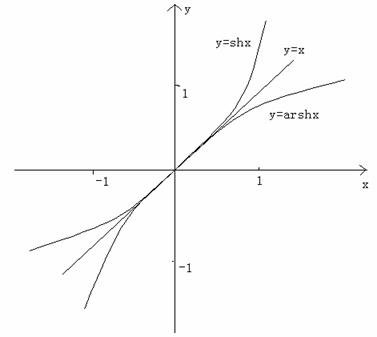
由于常见的缘故，我们常常需要讨论一些特定的复合函数，例如我们在工程领域常常遇到的一类自然指数通过特定的一些组合而得到函数，就是所谓双曲函数及其反函数,下面给出这些函数的定义以及图形，建议同学们仔细揣摩它们的性质，尽量从直观方面来熟悉它们：

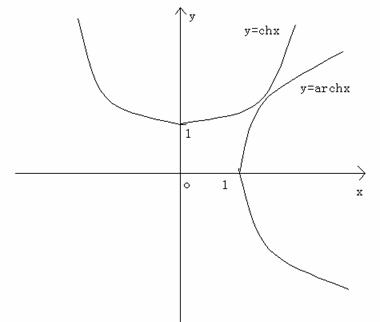
双曲正弦函数：；

反双曲正弦函数：；

双曲余弦函数：；

反双曲余弦函数：

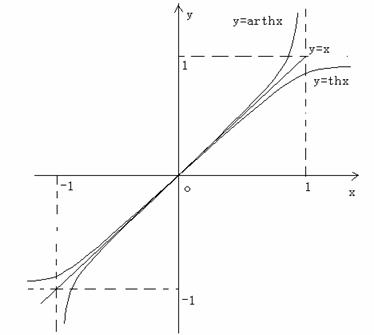
双曲正切函数：；

反双曲正切函数：

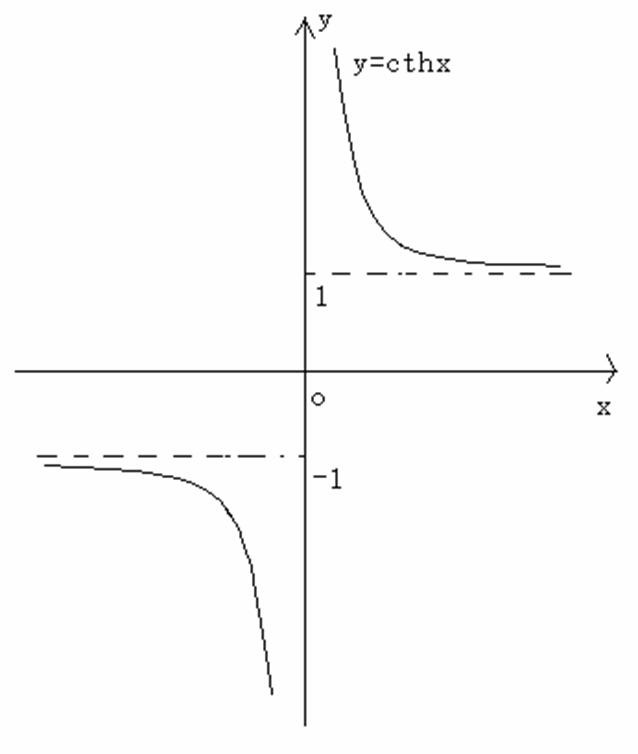
双曲余切函数：

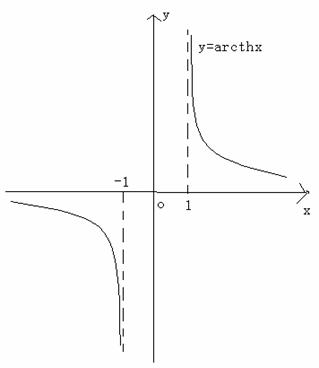
反双曲余切函数：

分段函数。

我们在实际问题中会经常遇到一种特殊形式的函数，它不属于初等函数，而是由一些在不同的定义域区间定义的初等函数组合起来的，这种形式的函数也许数学方面的意义并不是很大，但是实际意义还是很大的，特别是这种函数在分段点处，往往需要进行个别的研究，这常常是我们在后面的学习当中需要作为特殊情况加以处理的地方。

二，答疑解难。

1． 在函数有界性的定义里，M是唯一确定的吗？

[答]：不是。

在我们的有界性定义当中，只是指出了一个存在性的条件，即只要存在一个符合条件的M值，那么函数就是有界的。反过来，如果存在一个确定而有限的M值，那么我们总是可以让M加以任何一个正数，从而得到另外一个不同的M值，这就是说我们实际上可以由此而得到无数的M值。记住这里的关键是定义的存在性。

2． 周期函数的定义域必须是全部实数吗？

[答]：严格说来，周期函数的定义域应该是全部实数，因为周期性的实质，就是整个函数的图形沿着X轴进行一定大小的平移，而整个函数保持不变。而如果函数的定义域是实数集合上的有限大小的区间，那么这种平移肯定会使得函数的定义域发生改变，从而改变了原来的函数本身。不过在不过于严谨的情况下，可以通过一定的定义，使得我们只是着重于函数在局部的周期性，这样也就还是可以定义在局部区间的周期性的。

3． 一个周期函数的周期是唯一的吗？

[答]：不是唯一的。

很显然，如果已知一个周期函数存在一个周期T，那么至少2T也是这个函数的周期，初学者对周期函数往往只是对一个周期函数的最小周期有印象，而忽略了最小周期的任意整数倍都是周期这么一个简单的事实，而我们后面常常在一些解题技巧当中需要意识到这点。

4． 反函数就是把一个函数的自变量与因变量的符号进行互换而得到的吗？

[答]：错误。

初学者常常在这个问题上犯糊涂的主要原因，是不能很仔细地抓定义，抓概念，而是满足于望文生义，必定无法学好微积分。

反函数概念的核心在于，互为反函数的两个函数表示的并不是同一个函数关系，因为我们改变了关于因变量与自变量的观点，我们不能对同一个函数说，它既表示了y对x的函数关系，又说它表示了x对y的函数关系，因此至于我们习惯上写出显式来，并且交换自变量与因变量的字母，从而能够在几何上建立一个直观。

一般地，在我们学习任何概念的时候，关键是要建立起自己的对于一个抽象概念的直观方式，比方说反函数，如果能够牢固地抓住互为反函数的两个函数的几何图象的特征，即它们在直角坐标系里关于直线x=y对称，就有了一个思考的线索与途径。

5． 函数y=x²，（-6<x<10）是偶函数还是奇函数？

[答]：不对。

函数的奇偶性并不是只与函数形式有关，还与函数的定义域有关，即具有奇偶性的函数的定义域必定要求是关于原点对称的。

6． 单调递增函数的反函数为单调递减函数，对吗？

[答]：不对。

这里应该强调严格单调性，只有对于具有严格单调性的函数，才具有这样的性质。

7． 在幂函数里的x可以取负值，为什么指数函数里的a不能取负值？

[答]：在幂函数里的x可以取负值，是在一定的条件下，即其中指数的分母为奇数。这里指数为常数，因此只要确定了指数，函数也就确定了。

而在指数函数里，处于指数位置的x是自变量，这时函数的定义域就不再是完整的区间，变得很复杂，因此我们只考虑指数函数里的a大于0的情形。

8. 反三角函数是三角函数的反函数，对吗？

[答]：从严格的意义来讲，这么说是不严谨的。

因为当我们取反三角函数时，必须取三角函数的部分定义域，才能使得反三角函数满足函数的定义，因此只有与在定义域上相应作了限制的三角函数才具有反函数。