第九章．无穷级数
无穷级数。
整个微积分的根本目的就是构造研究函数的方法。我们已经知道如何利用极限，求导，微分这些基本的微积分方法，来直接研究一个函数，这里我们要讨论的是运用完全不同的一种思想方法，来研究函数的行为，这就是逼近的方法。
我们在进行函数的数值计算时，已经接触过逼近的思想方法，但纯粹数值逼近，得到的只是数值结果，对于我们要求了解函数的解析性质并没有直接的帮助，我们希望用解析的形式来逼近函数，一般就是利用比较简单的函数形式，逼近比较复杂的函数，最为简单的逼近途径就是通过加法，即通过加法运算来决定逼近的程度，或者说控制逼近的过程，这就是无穷级数的思想出发点。
形式地看，无穷级数就是用自然数编号的无穷多项的和式，每一项都是一个确定的解析式，也就是说每一项所在的项数唯一地决定了它的表达式形式，当然也可以是一个确定的数值，这就是常数项级数。
一般我们能够用一个统一的表达式即所谓通项来表述无穷级数的每一项，只要给出项数，就能根据通项唯一地确定这一项的表达形式。
对于任意构造的无穷级数，我们肯定能够给出加法运算结果的，只能是有限的和式，这就是部分和，部分和总是我们在考察整个无穷级数之前用以探测级数性质的对象。而我们考察一个无穷级数的另一个角度，就是考虑由一个无穷级数的所以部分和所组成的数列，或者是函数列。
最终，我们的目的是希望级数逼近某个确定的函数，或者说是以某个函数作为极限，因此，对于给出的无穷级数，最为关键的问题就是它是否收敛，然后就是收敛函数的性质，这就是我们研究无穷级数的中心课题。
无穷级数的收敛与发散性质。
首先我们只是考虑级数的敛散性的问题，也就是存在性问题，而不是如何求极限的问题。关于无穷级数的敛散性，有如下的基本性质：
1．任意改变一个级数的任意有限项的值，都不影响这个级数的敛散性。
原因很显然，只要对一个级数所作的改变是有限的，就不能使得这个级数，由趋向于无穷而变得趋向于有限，也不能使得这个级数由趋向于有限而变得趋向于无穷，或者是由根本不存在任何极限，而变得出现极限。
2．如果任意有限个无穷级数都是收敛的，那么它们任意的线性组合也必定是收敛的。
注意对于都是发散的级数，则不存在类似的结论。
3．在一个收敛级数的各个项之间任意地填加括号，得到一个新的级数，收敛于同样的和。
这可以看成是加法的结合律的一个推广。
4．级数收敛的一个必要条件是它的通项以0为极限。
即
收敛
。
正项级数及其敛散性判别法。
如果一个无穷级数的每一项都大于或等于0，则这个级数就是所谓的正项级数。
正项级数的主要特征就是如果考虑级数的部分和数列，就得到了一个单调上升数列。而对于单调上升数列是很容易判断其敛散性的：
正项级数收敛的充要条件是部分和数列有界。
有界性可以通过许多途径来进行判断，由此我们可以得到一系列的敛散性判别法。
比较判别法：
（1）一个正项级数，如果从某个有限的项以后，所有的项都小于或等于一个已知收敛的级数的相应项，那么这个正项级数也肯定收敛。
（2）而如果用来作比较的级数已知是发散的话，在同样条件之下，这个正项级数同样也是发散的。
如果说逐项的比较还有些麻烦的话，可以采用如下的极限形式：
对于正项级数和
，如果
，
即它们的通项的比趋向于一个非0的有限值，那么这两个级数具有相同的敛散性。
积分判别法：
对于正项级数如果存在一个单调下降连续函数f（x），有f（n）=un，那么级数与广义积分
具有相同的敛散性。
比值判别法：
设正项级数从一个确定的项以后，每一项都严格大于0，并且如果有
，
那么这个级数收敛，反之，如果从一个确定的项以后，每一项都严格大于0，并且有
，
则级数发散。
同样这种比较也可以采用极限形式：
设正项级数从一个确定的项以后，每一项都严格大于0，并且如果有
，
那么当C大于1，则级数发散，当C小于1，则级数收敛，如果等于1，则本判别法无法进行判断。
根值判别法：
对于正项级数，如果从某一个确定的项开始，都有
，
则级数收敛，反之，如果从一个确定的项以后，每一项都满足
，
则级数发散。
同样这种比较也可以采用极限形式：
设正项级数从一个确定的项以后，
，
那么当C大于1，则级数发散，当C小于1，则级数收敛，如果等于1，则本判别法无法进行判断。
绝对收敛级数。
实际上针对正项级数的敛散性判别法的有效范围还可以扩大，也就是说，还可以用于判断更多的级数是收敛的。这是通过引入绝对收敛的概念而得到的。
如果我们把一个任意项的级数的每一项都取绝对值，那么就得到了一个正项级数，如果这个正项级数是收敛的，那么这个任意项级数就被称为是绝对收敛的。给出绝对收敛这么一类任意项级数的好处，就在于
一个任意项级数如果是绝对收敛的，那么也就一定是收敛的。
绝对收敛级数不仅具有可以应用针对正项级数的敛散性的判别法的特性，还具有如下的性质：
（1）如果把任意项级数的所有正项都保持不变，而所有负项都更换为0，那么就得到一个正项级数
；如果把它的所有负项都改变符号，而正项都更换为0，则得到另一个正项级数
，然后就得到一个任意项级数的绝对收敛的充要条件，为正项级数与都收敛。
从这个性质能够得到一个推论，即
如果任意项级数绝对收敛，就有
=-。
作为加法交换律的一个推广，对于正项级数，如果任意改变它的各项的相加顺序，不会改变它的敛散性，同样，对于绝对收敛级数也有这样的性质，即
（2）对绝对收敛的任意项级数，任意改变它的各项的相加顺序，不会改变它的敛散性，并且是收敛于同样的极限。
不只是对于加法的交换律，对于绝对收敛级数的乘积也有性质：
（3）如果两个任意项级数都绝对收敛，那么它们的各项的乘积，按照任意方法排列而得到的级数同样绝对收敛，并且和为两个任意项级数的和的乘积。
交错级数。
考虑一种特别的级数形式，即相邻两项的符号相反，称为交错级数。交错级数具有一个简单的性质：
如果{
}为一个单调递减数列，并且以0为极限，那么通过改变这个数列相邻两项的符号而构造的两个交错级数都收敛。
这种级数称为莱布尼兹级数。
我们知道一个任意项级数，如果由它的各项的绝对值所得到的级数收敛，则原来的级数也收敛，如果发散，则原来的级数不一定也发散，如果反而是收敛，则称这种级数为条件收敛的。实际上，条件收敛的级数，可以通过变换级数各项的顺序而使得这个级数收敛于任意实数，包括无穷大。
幂级数。以及幂级数的收敛半径和收敛区间。
级数的每一项也可以是函数，这种级数称为函数项级数。
这里我们讨论一种特定的函数项级数，即由如下形式的幂函数组成的级数，称为幂级数：
。
也可以直接写成：
幂级数的敛散性具有很好的特征，即所谓阿贝尔定理：
如果幂级数在点x=k
处收敛，那么它在区间
内的每一点处都绝对收敛；反之，如果幂级数在点x=k处发散，那么对于不属于
的所有x都发散。
显然，上面的定理使得幂函数的收敛域只能是一个开区间，称为幂级数的收敛区间。收敛区间的长度的一半称为收敛半径.
应用对于正项级数的比值判别法和根值判别法的极限形式，可以求出幂级数的收敛半径。
设对于幂级数的系数，有
，
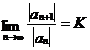其中K为有限数值或者是无穷大。
进一步，就有
，
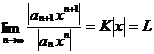则得到：
（1）
如果K大于0，则在L小于1时，幂级数绝对收敛，而L大于1时，幂级数发散，因此此时幂级数的收敛半径为1/K。
（2） 如果K=0，则对于任意的x幂级数都是绝对收敛的，因为此时L=0，小于1，这时可以认为幂级数的收敛半径为无穷大。
（3） 如果K为无穷大，则幂级数只在x=0处收敛，而取任意非零的数值时，级数都是发散的，因此可以认为幂级数的收敛半径为0。
类似地，也可以根据根值判别法的极限形式，得到相同的结论。
求出幂级数的收敛半径以后，即可得到相应的收敛区间和收敛区域。
幂级数的微分，积分，连续性。
我们知道对于一个幂级数，如果它的收敛半径大于0，那么在它的收敛区域内，就得到了一个确定的以这个收敛区域为定义域的函数，为这个幂级数的和函数，自然，对于这个和函数也应该能够应用微积分的方法加以研究。
首先是对和函数的求导：
如果幂级数的收敛半径r大于0，则它的和函数S（x）在（-r，r）上必定可微，并且导函数为
。
注意在上面的定理当中，和函数的可微区间是开区间，因为即使和函数在这个区间的端点可能有定义，这个定理也不能保证和函数在端点处具有可微性。
和函数还具有连续性：
如果幂级数的收敛半径r大于0，则它的和函数S（x）在其定义域上连续。
注意，对于连续性，定理强调的是在它的定义域上，也就是包括有定义的端点。
连续性也就意味着可以对幂级数逐项求极限。
此外，幂级数还可以逐项求积分：
如果幂级数的收敛半径r大于0，则它的和函数S（x）在其定义域上的任意一点x处都有
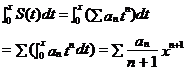
幂级数展开与应用。
幂函数应该说是最为简单的初等函数，我们研究幂级数的最终目的，就是希望运用幂级数这种无穷和式的形式来逼近比幂函数更为复杂的函数。反过来的问题，就是给定了一个函数，如何找到一个幂级数来逼近它，这就是幂级数展开的问题。
前面在微分的应用当中，我们实际上已经接触了幂级数展开的问题，就是泰勒公式。不过我们并没有仔细讨论。
现在根据级数理论的有关概念，可以知道所谓函数f（x）在a点可以用幂级数展开，即
这个表达式能够成立，就是对于收敛区间（-r，r）内的x，余项趋向于0。否则幂级数就是发散的，或者是它的极限和函数不是f（x）。
一般是实际应用当中，我们常常取基点a为0，这样取a为0所得到的泰勒展开式也称为马克劳林级数。
下面列出基本的泰勒展开式。
（1）
的展开式。
。
（2）sinx的展开式。
Sinx=
。
（3）二项式
的展开式。
=
。
从这三种最为基本的函数展开式，结合几何级数的求和公式，可以得到很多的函数的泰勒级数展开式。
我们既然可以应用幂级数这样的展开式来逼近函数，有可能的话，也可以反过来把一个数项级数理解为一个幂级数展开式，这样求数项级数的和，就可以转化为求幂级数展开式所对应的一个函数在某点的函数值。
另外，幂级数不仅只是应用于解析逼近，还可以应用于数值近似计算。
三角级数以及三角函数系的正交性。
完全由三角函数系
，（k=0，1，2，…）组成的无穷级数
就是三角级数，如果这个级数对任意x都收敛，那么得到一个确定的和函数f（x）为
f（x）=。
把上面的等式两边同时乘cosnx或者sinnx，并且在
上积分，就得到如下的可以确定级数系数的公式：
，
，（k=0，1，2，…），
这样，对于一个函数f（x），运用上面的公式，就可以构造相应的三角级数的展开式，这种三角级数就是所谓的傅立叶级数。
之所以要把函数展开为傅立叶级数，是因为三角函数系具有非常特别的性质，就是所谓的正交性。
我们说两个函数在某个区间上是正交的，就是这两个函数的乘积在这个区间上的积分为0，而三角函数系里的任意两个函数在某个区间上正好都是正交的。
对于三角函数系，正交区间为
；
对于三角函数系
，正交区间为[-l，l]。
周期2
函数的傅立叶级数。
从傅立叶级数的构成可以看出，和函数必定也是以2为周期的周期函数，因此我们就可以对任意以2为周期的函数，考虑把它表达为傅立叶级数的形式。
按照上面的系数公式，可以写出一个以2为周期的函数的傅立叶级数形式，但是否这个级数一定收敛于这个函数，则是这种构造方法本身不能说明的，因为给出系数公式的前提，就是假设存在这么一个级数是收敛于它的。因此还需要下面的傅立叶级数收敛的充要条件：
如果周期为2的函数f（x）在长为2的闭区间上分段光滑，那么它的傅立叶级数在这个区间上的每一个连续点处都收敛于这个函数，而在每一个跳跃间断点处，都收敛到
。
这个定理可以看成是存在性定理，没有这个定理，我们只能在假设存在一个傅立叶级数表达形式的前提之下，形式的写出来，至于是否收敛到这个函数，则是不一定的，因此这个定理具有关键的作用。
然后，我们需要更进一步地给出傅立叶级数形式与它所表示的函数之间的等价性，也就是唯一性：
如果两个形式相同的傅立叶级数趋向于同一个和函数，则两个傅立叶级数的相对应的系数分别相等，也就是说，和函数与一种形式的傅立叶级数是一一对应的。
既然完全可以把一个傅立叶级数和它所表示的和函数等价看待，那么对于傅立叶级数也应该可以应用微积分的计算，即可以求积分与求导函数：
（1）任意一个傅立叶级数，无论它是否收敛到它所对应的和函数，都可以通过在任意两个积分限之间逐项积分，得到一个新的级数收敛于对应和函数的相应积分。
（2）如果f（x）是以2为周期的连续函数，并且它的导函数在长为2的闭区间上分段连续，那么对f（x）的傅立叶级数逐项求导，就得到f（x）的导函数的相应傅立叶级数。
周期2l函数的傅立叶级数。
如果函数不是以2为周期，而是任意的别的周期，则根据周期函数的性质，运用适当的变量替换，就可以变换到以2为周期的函数的情形。
因此类似地，我们可以得到经过变换的三角函数系；
相应的傅立叶级数表达式
f（x）=
；
相应的系数公式
，
，（k=0，1，2，…）；
这样得到的傅立叶级数同样具有前面的傅立叶级数所具有的性质。
最后，我们简单地讨论一下如何把有限区间上定义的函数展开为傅立叶级数的问题。
（1） 如果函数定义在一个周期长的区间上，则可以直接作周期开拓，也就是取一个周期函数，使得它在给定区间上与原来的函数一致，然后对这个新的函数作傅立叶级数展开，得到的级数即可作为原来函数的开拓。
（2） 如果函数定义在半个周期长的区间上，可以有两种处理方式。一是把原来的函数补充为偶函数的形式，再按照（1）的步骤进行开拓，这种方式得到余弦函数的展开式。
（3） 二是把原来的函数补充为奇函数的形式，再按照（1）的步骤进行开拓，这种方式得到正弦函数的展开式。
二，答疑解难。
如果一个任意项级数不是绝对收敛的，那么它是否一定是发散的？
[答]：不对。
初学者往往因为绝对收敛就一定收敛而得到绝对收敛与收敛等价的错误印象，实际上，绝对收敛是收敛的充分条件，而不是必要条件，因此反过来说是错误的，正因为这点，才有了条件收敛的概念，因此我们应该认真体会这点，才能很好地理解条件收敛的概念，而条件收敛对于初学者来说，是比较困惑人的。
我们讨论如下几个问题。
1．对于正项级数，如何选择恰当的敛散性判别法？
[答]：（1）首先如果通项不趋向于0，则级数肯定发散。
（2）考虑部分和是否关于n有界，如果有界则收敛，如果无界则发散。
（3）一般说来，如果正项级数的通项中含有阶乘，指数函数，幂指函数等因式，则一般首先考虑使用比值判别法。
（4）如果正项级数的通项中含有指数函数，幂指函数等因式，但不含义阶乘，那么可以考虑使用根值判别法。
（5）对于以n的幂有理式为通项的正项级数，不管是整数幂还是分数幂，由于n趋向于无穷大时，通项关于无穷小1/n的阶比较容易观察，因此一般考虑使用和p级数作比较。
（6）如对于通项为幂有理式的级数，由于前后两项的比值的极限或者通项n次根的极限都是1，所以比值判别法或者根值判别法都会不起作用，不过，如果通项另外还带有幂有理因式，则这两种判别法都还是有用的。
2把初等函数展开为幂级数的方法。
[答]：一般常用的方法有：
（1）通过把函数进行变换，转换，从而尽量作到能够利用已知的展开式。
（2）运用逐项积分或者逐项微分法来展开。
（3）运用待定系数法。
（4）计算某些特定点的各阶导数，然后利用泰勒级数来展开。
（5）运用级数的运算法则，从已知的级数展开式得到要求的级数展开式。