第一章.质点运动学
质点及其概念的起源。
我们能感知到运动,这似乎已经是对我们的主观观念作物理学分析的最初始的起点了。从这里出发,在远古的时代,人类已经开始有了特定的对一些自然事物的运动的描述。例如人类最早进行的科学活动—天文观测,就是描述各种天体在天空的运动轨迹。
这时,人们已经意识到点是描述运动时的基本对象。而实际上,作为一个概念的点是人类的抽象思维的最早产物之一,它作为几何概念,人们逐渐发现并不需要给它赋予实际的物理意义,而只需要应用它来描述物体的位置即可。这样,当人们具备了应用数字来描述在时间与空间中进行的测量的能力后,运动学就开始以几何学的面貌出现并逐渐发展起来。
然而,在另一方面,一个点只是纯粹的几何概念,还不足以表达作为运动的物体的属性,这就要求这个点还具备一种反映其运动属性的物理性质,这就是后来所明确的概念—质量。从而得到质点的观念—也即具备一定质量的几何点。
运动方程。
从几何的角度建立一套描述质点在每一时刻所处位置的运动学方法,这就是建立运动方程。
所谓运动方程,是建立在这样一种观念之上的:只要能得到质点在某一时刻的完备的运动状态,就决定其在某一确定外界环境下,此后任一时刻的完备的运动状态。这就是所谓物理意义上的因果律。因此运动方程的含义即是由质点在某一时刻的完备的运动状态,求解其在某一确定外部环境下任意其他时刻的质点运动状态。
那么,怎么样才能被称为是对一个质点在某一时刻的完备的描述呢?这就要求有描述在某一时刻的运动属性的物理概念,直观上就是用来描述运动的快慢,以及快慢程度本身的变化情况。这就得到了:
瞬时速度和瞬时加速度。
所谓瞬时的观念来源于微积分的描述函数局部的变化性质的导数的观念,从物理上讲,我们可以通过提高对时间间隔的测量分辨能力,来得到对瞬时的逼近,而这个概念的合理性正是建立在我们经验的认可上,也即我们的直观经验里的对时间与空间的连续性的假定,在我们需要处理的问题里都是很合用的。这样在描述运动时,就可以把位移和时间作为连续变量来处理。
设质点A在时刻t的位置可以用位移矢量L描述,从t开始,行进了Δt的时间后,到达L+ΔL处,这样质点在L处的瞬时速度就定义为
v=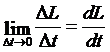
而质点在L处的瞬时加速度定义为
a=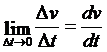
其中Δv指质点在L处和L+ΔL处的瞬时速度的矢量差。
在不会引起混淆的情况下,瞬时速度有时也简称为速度,瞬时加速度有时也简称为加速度。
对于初学者来说,瞬时并不是一个能很好掌握的抽象概念,在任何一个时刻,不管质点的运动状况如何,它的位移肯定为0,然而它的速度却可以不是0,它的加速度也可以不是0,表面上,这似乎是很难理解的,实际上对于某一时刻的质点,如果我们只是知道它的位置,那么我们就无从知道它在接下来的任意小的时间间隔后,会到达什么位置。这就是说,在这一时刻它的位置还不是对它的运动状态的完备描述,要想知道它在接下来的任意小的时间间隔后,会到达什么位置,就必须知道质点在这一时刻的瞬时速度,以及瞬时加速度(如果不为0的话)。
初学者可能会提出一个有趣而又难以回答清楚的问题,即是否还存在瞬时加加速度呢?实际上,在我们学习了牛顿运动定律以后,就会知道我们只需要考虑到位移对时间的二阶导数—加速度即可,而三阶或三阶以上的导数都是意义不大的。也就是说,由于物理的原因,对质点运动的描述—运动方程里不会出现二阶以上的位移对时间的导数。
至此,我们已经可以大体得到一个运动方程所具有的形式:
L=f(L0,v0,a0,t0,t)
其中,L0,v0,a0是质点在初始时刻t0的位置矢量,速度和加速度。它们构成质点在初始时刻的运动状况的完备描述。而函数f则由质点在初始时刻的运动状况决定了其在此后或此前的任意时刻t的完备运动状况。
我们知道所谓运动方程的含义是,给出一定的初始条件后,由运动方程可以求出质点在合理时间范围里任意时刻的质点的位置。
那么,物理学的运动方程就和几何学的曲线方程有所异同:
首先对于运动方程,取定时间t,就必须可以求得在这一时刻质点的位置矢量,如果质点是在平面上运动,那么它的位置矢量就是二维的,也就是说有两个分量,比方说在x轴和y轴上的分量,这样要求出两个未知数,则要求能分别在两个不同方向上建立运动方程。类似的,如果质点是在三维空间里运动,就需要在三个不同方向上建立运动方程。有时如果要求的是一个具有几何特征的位置量,而这个位置量又可以完全由它的几何特征决定,并不一定非得要由时间来决定,例如下面的例题1里的最高点和水平落点,那么可以对运动方程组进行消元,消去时间t,从而得到质点运动轨迹的纯粹几何的曲线方程。再从曲线方程求出其特定的几何特征量。
可见,曲线方程是不含时间的,也即从曲线方程我们无从由时间求得在这个时刻得质点的位置,至于解析几何里常用的曲线的参数方程,尽管也常引入时间作为参量,但是是一律假定质点在运动轨迹上作匀速率的运动,显然这是在数学的角度上够用的方便假定,却完全不考虑实际的物理过程,因而不能作为运动方程来使用。
对于初学者来说,清楚地区分这点是非常重要的。因为在许多复杂的情形下,需要非常小心才能得到运动方程的完备表述,这时经常容易发生的错误就是混淆运动轨迹的几何描述和运动学描述,在下章,我们还需要学会进行动力学描述。
下面我们讨论几种简单的运动:
直线运动。
质点在直线上运动时,它的位移矢量保持在同一条直线上,因此除了有相反的方向外,不会有其他的方向变化。由此质点的速度和加速度矢量也是保持在同一条直线上的。所以我们在处理直线上的运动时,只需要作代数运算即可,不过一定要仔细确定好各个矢量的正负号。
最简单的直线运动就是速度保持不变的匀速运动,这时速度一直保持为0或某个常值。对于这种运动,质点的初始位置和速度就完全描述了质点的全部状态,我们有
x=x0+vt。
如果速度在运动过程中发生了变化,那么我们就需要用加速度来描述这种变化。在这种情形下最简单的情况是加速度保持不变,而质点的初始状况就比匀速直线运动要复杂了。
这时质点的初始状态分别由初始位置和初始速度描述,而初始位置和初始速度的方向可以相同,也可以不同,这时最容易发生的错误就是符号规定的不一致,因此处理问题的一开始,我们就要把符号统一规定好,做题过程中不要发生混乱。已知质点的初始位置,初始速度,以及质点运动过程中的恒定加速度,我们有
x=x0+v0t+at2/2。
实际问题里,已知的初始条件要更多样化一些,但无非是五个物理量:位移,初始速度,加速度,时间,运动过程中的任意瞬时速度。根据这五个物理量的缺少情形,加上上面的方程,我们分别有五个方程:
v=v0+at
v2=v02+2a(x-x0)
x=x0+(v0+v)t/2
x=x0+vt-at2/2
这样,我们就基本完全地解决了直线上的匀加速度问题。
自由落体运动。
自由落体运动是我们日常生活中最常见的匀加速直线运动。以后我们学习了牛顿万有引力定律后就会知道,在一定的高度范围内,把自由落体运动看成匀加速度直线运动是非常好的近似。从这个例子我们可以很深刻地体会到物理学里取近似的重要性。从本质上来说,物理学定律永远都是某种程度的近似,关键在于这种近似是否够用。
把上面的方程用g替换a,即可得到描述自由落体运动的全部方程。
要注意的是,并非只有初始速度为0的自由落体运动才是自由落体运动,具有非0的初始速度的垂直方向上的运动,只要在运动过程中,只受重力的作用,就是自由落体运动。这点我们在下章可以更清楚地理解到。
质点在平面上的运动。
我们已经学习了矢量的分量表示方法,而平面上的矢量总是可以表示为两个不同方向上的矢量分量的和。因此平面上的运动总是可以归结为两个直线运动的和。在这个意义上,平面和空间里的任意运动学问题原则上都可以很好的解决。
这里涉及到一个重要的物理学原理,即
运动叠加原理。
运动叠加原理的实质就是矢量的加法运算。而矢量加法刻画的正是线性叠加的观念。在物理学里,我们会大量的遇到满足线性叠加律的物理量,物理学家们也习惯于用线性的物理量来逼近非线性的物理量,甚至可以说这是物理学的一个基本方法。而从数学的角度来讲,对于线性问题,已经有了近乎完美的解决方法,对于非线性问题,则困难重重,仍然缺乏统一而有力的处理方法。
我们要理解运动叠加原理,完全可以直接从矢量加法的角度来理解。在力学中,一个力学量,只要它可以用矢量来刻画,就可以在不同的方向上把它分解成分量的形式,分量的个数取决于这个矢量的维数,而每个独立的分量总可以看成是对一个独立的物理过程的描述。这样,任意的运动总可以分解为一些相互独立的,相对简单的运动分量。从而把对复杂运动的研究归结为分别对一些简单运动的研究。反过来也一样。这就是矢量给研究问题带来的好处。也是我们研究物理问题时,经常首先要考虑的一个原则。
目前,我们只研究几种特别简单而又典型的平面运动。从这里出发,可以了解很多由这些简单运动叠加起来形成的复杂运动。
抛物运动。
抛物运动实质上就是水平方向上的匀速直线运动和垂直方向上的自由落体运动的叠加。这样对于任意的抛物运动,关键在于把它的水平分量和垂直分量分解清楚,分别予以考虑即可。
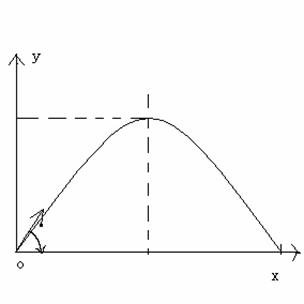
这里涉及到的几个问题是
(1)分别写出抛物运动的水平运动方程和垂直运动方程后,这两个方程是含时间变量的运动学方程,也即它们描述了质点随时间而发生的位置的变化。如果通过消除时间变量而把两个方程合并为一个方程,得到的是一个不含时间变量的几何曲线方程,通过这个方程可以得到一些具有几何特征,同时又具有物理意义的质点的特定位置量,但这么一个曲线方程本身并不是质点随时间而进行的运动规律。这种差别一定要理解清楚,否则一旦遇到复杂的运动问题,就会忙于建立方程而迷失于问题的物理意义。
(2)运动的几何特征。
首先相应于自由落体运动的上升于下降的对称性,抛物运动也具有以过最高点的垂直轴为对称轴的水平对称性,从而可以简化问题的计算。
还有一种对称性,就是对于具有相同大小并且都有向上分量的初始速度的两个质点,如果它们对水平方向的角度加起来为直角的话,那么它们在回到初始水平位置时,将飞行同样的水平距离。
然后,就是抛物运动的最高点和最远点这一类几何特征位置,抓住它们的几何特征往往能很简单地解决问题。我们在下面结合例题予以说明。
匀速圆周运动。
匀速圆周运动同样是我们日常生活中非常常见的运动形式,它的关键特征就在于它运动的速度矢量和加速度矢量大小保持不变,而方向总是保持相互垂直。而它的难点就在于怎么理解它的速度与加速度。
如下图所示,质点在时刻t1时的位置为a点,在时刻t2时的位置为b点,若取圆心O为坐标原点,那么位置矢量Oa和Ob的差的方向在Oa和Ob之间的角度趋向于0时,也就是t2趋向于t1时,趋向于过a点圆的切线方向,根据速度的定义,这就是图中的速度矢量A的方向,再考虑分别在a点和b点的速度矢量A和B,考虑到这是匀速圆周运动,质点的速度大小保持不变,那么它们的差A-B的方向在a和b的距离趋向于0时,必趋向于与过a点的半径的方向平行。根据加速度的定义,这就是质点在a点
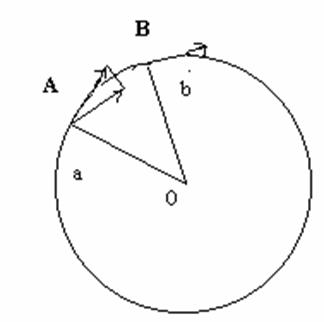 图1
图1
处的加速度的方向,同样是指向圆心的。
通过以上分析,我们确定了质点的匀速圆周运动的速度与加速度的方向,下面我们分析它们的大小。
由于是匀速圆周运动,因此速度大小保持不变。而加速度的大小则可以根据加速度的定义,由图1中所示的几何关系,给出速度差的表达式,其中包含变量为两个速度之间的夹角Δθ,再把加速度表达式中的Δt按角速度或线速度的定义,换成变量Δθ,取这个表达式在夹角Δθ趋向于0时的极限,就可以得到加速度的大小
a=v2/r=ω2r。
其中r为圆周的半径,v为质点运动的线速度,ω为质点运动的角速度。
我们还可以运用矢量对时间求微商的方法直接给出微商的表达式,从而同时给出了速度和加速度的方向和大小。
至此,我们可以归纳出匀速圆周运动最主要的特征就是速度与加速度的方向保持垂直,而大小保持不变。
掌握一种运动的规律,最主要的就是抓住运动过程中速度矢量与加速度矢量的关系。回顾一下我们所学的几种简单运动:
自由落体运动的加速度的方向和大小都保持不变,而速度大小总在变化,方向也可能在一点上发生正负的变化。
抛物运动的加速度同样保持大小和方向不变,而速度的大小和方向则总在发生变化。
至于匀速圆周运动,速度和加速度的大小都保持不变,而方向总在发生变化,但它们的夹角总保持为垂直。
在下章,我们会看到这些运动特征后面都是有物理原因的。
参照系和相对运动。
回到我们对运动的观察本身上来。我们在上面所进行的对质点运动的描述,是反映了我们对运动的观察,可是我们对同一个运动的观察,有可能因为我们观察者的自身的运动状态的不同,而得到不同的结果。自古以来人们已经考虑到这个问题。这就是参照系观念的起源。这实际上就提出了一个问题,既然我们在上面所给出的运动学描述都依赖于观察者所在的参照系,而我们又认为物理学规律应该不依赖于我们观察者的状态,那么那些运动学描述还是不是物理学规律呢?
应该说,运动学描述表示了在任意规定范围内的时刻,质点所在的空间位置。而我们的所谓运动学问题,总是从已知的一个运动学描述求另外的一个运动学描述,这里每一个描述都肯定是完备的,也就是说,在规定范围内质点的每一个时刻的运动状态是确定了的。我们需要求解的只是质点的运动状态里的一些特定的物理量值。实际上我们还没有涉及到运动的物理原因,也即我们还不能处理有关质点运动的一般问题,这需要我们学习了牛顿运动定律后才能进行的。因此我们看到所谓运动学描述还是非常几何性的描述,因此我们不能指望运动学描述具备与参照系无关的性质。而参照系之所以影响我们的运动学描述,也就是因为要考虑参照系本身的运动学状态。
由于参照系对于我们的运动学描述而言的意义,只是在于参照系自身的运动,因此实际上在处理不同的参照系导致不同的运动状态描述的问题时,面临的就是一个运动的叠加的问题。
我们在一个参照系里对一个运动进行观察,意味着我们观察者本身是在参照系里静止不动的,一旦我们作为观察者有了运动,我们的观察结果实际上就必须由原来的观察结果叠加上观察者的运动。这样,同一个运动对于不同参照系而言,其各自描述的不同正是反映了各个参照系本身运动状态的不同,而不是说那个运动对象本身有何变化。
因此在处理涉及到参照系发生变化的问题时,首先抓住一个能够最容易对运动进行描述的参照系,给出运动方程,然后再考虑其他参照系在第一个参照系里的运动。也就是说,所谓参照系之间的相对运动,总是可以把每个参照系都看成一个刚性坐标架,在每个参照系里都使用相同的时钟,(在狭义相对论里,我们会看到这些假设是有限制的。)这样在每个参照系里对于同一个运动对象都有各自的运动方程描述,同时对每个参照系而言,其他参照系作为一个刚性坐标架都有它在这个参照系里的运动描述,这样对运动对象的这些不同运动方程之间的形式进行变换,无非是对不同参照系运动状态的叠加而已。
直线上的相对运动。
如果问题中涉及的运动对象和参照系的运动都是在同一条直线上,那么无论取其中哪个对象作为用来观察其他对象的运动状况的刚性坐标架,所涉及到的运动描述的变换就是速度和加速度的代数运算,关键在于确定好直线的正负方向,然后再以此为依据,确定在这条直线上的速度和加速度的正负号。
平面上的相对运动。
分析平面上的相对运动,初学者应该学会动手画图,把各个参照系都用刚性坐标架的形式画出来,再分析所要研究的运动对象在各个参照系里的运动状态,最好的方法是在每个坐标系里都把对象的运动按分量的形式来考虑,这样在不涉及坐标系的旋转的情形下,就可以把平面问题归结到直线上的问题。下面我们将结合具体的例题进行分析。
二,疑难
1. 什么情况下我们可以把要研究的物体看成质点?
[答]:如果我们对于物体的描述与对于一个质点的描述所使用的变量数目和方程数目,可以做到一样,那么就可以把这个物体看成一个质点。更具体地说,如果物体中的所有点的运动轨迹总是保持相互平行,或者,我们只考虑物体的平动,而不考虑物体的转动,这些情况下,我们都可以把物体看成是一个质点。
2. 位移与位矢有何区别?
[答]:位矢是从坐标系原点到质点所在位置的矢量,这个矢量是和坐标系有关的,或者说,是和我们观察质点位置时我们自己的位置有关的。
位移是质点自身运动过程中,两个不同位矢的差,是从质点的一个位置指向另一个位置的矢量,这个矢量与坐标系的选择没有关系,是独立于坐标系的物理量。
3. 什么情况下位移和路程的数值是一样的?
[答]:首先位移是矢量,而路程是标量,一个位移具有确定的一个方向,它刻划的是两个空间位置(点)之间的最短距离,而路程则是表示物体运动过程中所经过的实际距离,或者说是它的运动轨迹的长度,那么只有在物体的运动轨迹就是空间两个位置之间的最短距离的路径时,才使得位移和路程在数值上相等。
4. 什么情况下平均速度和平均速率的数值是一样的?
[答]:有必要回顾一下平均速度与平均速率的定义或者说计算方法,首先记住,平均速度根本不涉及运动的具体细节,如果要求质点运动轨迹的两点之间的平均速度,就只是与质点在这两点的位置矢量,和质点在这两点之间的运动时间有关,用质点在这两点之间的位移除以质点在这两点之间运动所花的时间,就是平均速度。可见,平均速度与质点在这两点之间的具体运动路径无关,无论质点的运动路径如何,只要所花的时间一样,平均速度就是一样。
而平均速率则不同。平均速率是用两点之间质点所经过的实际路程除以所花的时间,这样平均速率就与质点的运动细节有关,两点固定,时间也固定,则平均速度就确定了。然而平均速率却是完全可以发生变化的。如果质点在这两点之间所经过的路程越长,则平均速率越大,反过来,如果质点在这两点之间所经过的路程越短,则平均速率越小,平均速率最小的时候,就是质点在这两点之间沿着直线运动,这时无论质点的运动过程中的速率发生什么变化,最终的平均速率都和平均速度大小一样。除此之外,平均速率都要大于平均速度的数值。
那么我们就得到了答案,就是只要质点在两点之间的运动轨迹是直线,就会有平均速度等于平均速率。
5. 瞬时速率和瞬时速度的关系。
[答]:从上面我们分析速率与速度的不同,就可以得到启示,就是速率与具体的路径有关,而速度与具体的路径无关。这样到了瞬时的情况下,都不涉及路径,那么它们的产生差异的地方就不存在了,因为在瞬时的情况下,位移与路径的微元都是直线微元,两者没有差别,这样两者只剩下标量与矢量的差别,即瞬时速度的大小与瞬时速率相等,而瞬时速度有方向,瞬时速率没有方向。
6. 合成运动与相对运动的异同。
[答]:这两种运动在本质上应该是一回事,不过在我们做题时,还是作些区分更有利于快速而正确地完成题目。
合成运动一般指一个物体的运动可以看成是同时参加了两种运动,这两种运动对于观察者来说,可以分别描述它们的状态,因此对着两种运动进行矢量加法就可以得到合成的运动。
相对运动是指对于同一个物体的运动,在两个不同的参照系里进行观察,因此对于同一个物体的运动具有两种不同的运动学描述,这两种不同描述可以通过两个不同参照系之间的变换而相互推导出来。
在作题时,首先区分这两种情况以便于建立清楚的物理图象。
7. 为什么匀速圆周运动的瞬时加速度的方向为指向圆心?是否所有的圆周运动的瞬时加速度方向都是指向圆心?
[答]:初学者对于加速度定义为速度对时间的变化率的第一反应就是大小的变化,首先对于匀速圆周运动具有瞬时加速度就不能很直观地把握到,所以应该对于速度的矢量性质认真地加以体会,理解只要速度的大小或者方向有了变化,就是速度有了变化,匀速圆周运动的速度大小固然没有变化,方向却是随时都在变化的。因此一定存在反映速度方向变化的加速度。
那么如何表示这个加速度呢?仍然是根据速度的矢量性质和加速度的定义,速度的矢量差的方向就应该是加速度的方向,这时希望同学们动手画一下草图,看圆周上匀速运动质点的速度差的方向会有一些什么样的情况,就会知道只有定义瞬时加速度,才会有容易确定的方向,而瞬时加速度的方向之所以容易确定,是因为瞬时加速度的方向是作为一个极限的。
初学者对于方向的极限可能难以理解,觉得圆周上两点趋向于接近,则它们的速度差趋向于0,那么加速度也应该趋向于0,趋向于0的加速度如何具有方向的呢?这就是没有领会取极限过程的含义。
记住:我们对于极限过程,应该理解为一个运动的过程,而不是静止的。速度的矢量差的极限,绝对不能理解为两点合并到一起时的矢量差,而是两点永远没有合并到一起的矢量差的方向的一个变化趋向。显然这个方向变化的趋向就是指向圆心的,这个过程类似于微积分里单调有界函数的极限过程,请同学们仔细体会这里如何应用微积分的这个定理。
反过来推理,所有的圆周运动肯定具有指向圆心的瞬时加速度,因为纯粹改变运动方向的瞬时加速度肯定指向圆心,但如果同时存在改变运动速度大小的瞬时加速度,则必定是与瞬时速度的方向一致,这样质点运动就同时表现出两个瞬时加速度,这意味着质点的瞬时加速度应该是两个瞬时加速度的矢量和,这样一来,就不会是指向圆心的了。
这里涉及到一个很重要的方法,就是建立随动坐标系,对矢量进行分解。
所谓随动坐标系,就是坐标系原点就是运动质点本身,而这个坐标系的方向根据质点运动的某个特定方向来定义。
如下所示,就是一个在固定轨道上运动的质点的一种随动坐标系:
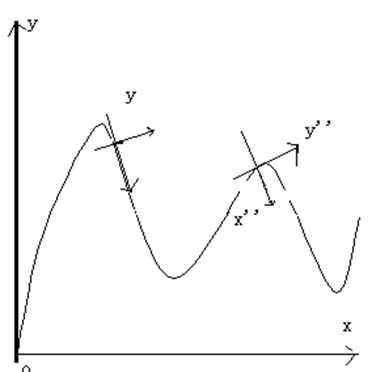
在这个圆周运动的例子里,随动坐标系原点就建立在运动质点上,X轴的方向与质点运动方向一致,这样,就可以在这个坐标系里进行有关质点运动的矢量分析,从而解决非常复杂的运动问题。