第十章.静电场中的导体与电介质

大量的电现象都涉及到电场中的物质由于电场的作用而发生的现象，不仅是自然界广泛存在，而且在我们认识到这里的物理规律后，更是广泛的应用于电气设计与电子器件。本章我们就要依据电场对电荷的作用这样的基本规律，来分析各种表面看起来似乎非常复杂的电场对宏观物体的作用。

 

电场中的导体。

在静电场中的导体总会达到一种平衡状态，就是所谓静电平衡的状态。在这种状态下，导体的内部与外部都不存在电荷的宏观运动。由于导体的性质就是电荷的自由运动，因此这种状态实际上就意味着

（1）导体内部的电场强度处处为0，而导体表面的电场强度的方向总是和导体的几何表面垂直。否则，很显然就会出现电荷的宏观运动。

（2）导体任意位置的电势都相等，显然如果不是这样的话，同样也会出现电荷的宏观运动。

这样一种状态的导体具有一些特定的性质：

（1）最主要的特征就是导体的内部和表面具有完全不同的特点，即在导体的内部所带的净电荷为0，而如果导体带电的话，也只是分布在导体的外表面。这是由于在外部电场的作用下，导体的自由电荷在电场力的作用下运动，而又受到导体表面的约束，从而停留在导体的外表面，建立了一种动态平衡所导致的结果。

（2）建立平衡后稳定下来的导体，电荷面密度的大小与该处的表面曲率成正比。

（3）导体表面附近真空的电场强度的大小为该处的电荷面密度和真空介电常数的比值，方向为垂直于导体的外表面并向外。

电场对导体的这种作用，能使电场中的空腔导体产生非常有趣的现象：

（1）当空腔内不含带电体时，空腔导体就只是在外部电场的作用下，这时由于导体在电场中的独特性质，使得空腔内部的电场强度为0，同时电荷也不会分布在空腔内表面，而只是分布在空腔外表面。

（2）当空腔体内含有带电体时，导体本身内部的电场强度仍然为0，空腔内由带电体激发的电场与空腔外部的任何电场没有关系，完全由空腔内的带电体决定，并且导致空腔内表面产生与空腔内部所包含电荷异号等量的电荷。而空腔外部的任何电场只决定于空腔外表面的电荷分布，

可以看出空腔导体使得其内部与外部完全隔绝了电场的相互作用，这种性质非常有应用价值。

即一方面可以使得空腔内部不受任何外部电场的影响，另一方面如果使空腔导体接地，则任何空腔内部电场所激发的分布在外壳的电荷都可以被释放，从而对空腔外部不产生任何影响，而在内表面激发的电荷就只是局限于内表面上。这样就起到了静电屏蔽的作用。

 

电场中的电介质。电介质的极化

所谓电介质就是相对于导体而言的，即内部电荷被拘束，从而不能有宏观运动，但一般仍然会出现微观的运动，如分子的转动，这样就导致极化现象。

对于极化现象，我们必须强调与静电感应现象的物理实质上的区别，这两种现象在表面看来是很类似的，但静电感应所产生的电荷是导体内部的自由电荷，而极化现象中出现的分布在导体两个相对表面上的电荷则是束缚电荷，它们都是内部电荷对外部电场的反应，但它们形成内部电场的方式不同。

电介质的组成分子通过微观运动而形成内部电场的机制有两种情况，一种是有极分子转动产生的极化，一种是无极分子通过微观位移导致的位移极化，而静电感应则是内部自由电荷从一个表面到另一个表面的长程运动。这两种现象的感应和极化程度都和外部的电场强度相关。

由于极化的实质就是电介质内部电偶极矩的产生，因此为了刻划电介质的极化程度，我们给出一个物理量就是描述电偶极矩的“密度”。这就是电极化强度矢量P，定义为体积元内所有电偶极矩的矢量和。

对于一个在外部电场作用下的电介质，其内部的合电场强度是外加电场强度和内部极化电荷产生的电场强度的矢量和，这个合场强与电极化强度矢量存在一个实验归纳性质的唯象关系，即合场强与电极化强度矢量成正比，比例系数为真空介电常数和电介质的电极化率的乘积。所谓电极化率是反映材料属性的一个实验数据，必须通过实验测量得到，而不能通过其它方法计算得到。

 

介质中的高斯定理。电位移。

我们上面讨论的高斯定理是在真空的情形，那么在介质中，由于增加了附加电场，高斯定理就必须作一些推广。

首先任何静电场都肯定满足高斯定理，但由于介质中的等效电荷在实际问题中并不容易求出，因此我们必须引入一个新的起辅助作用的物理量D，使得：

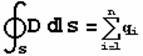
我们称D为电位移矢量。

这样我们就避免了求极化电荷，从而利用这个推广的高斯定理来求解介质中的场强。

我们得到一般的求解介质中的场强的方法：

我们能解的问题要求自由电荷的分布是均匀对称的，电场的分布也是对称的，介质必须是均匀各向同性，充满电场所在的整个空间，或者充满等势面之间的空间。然后就可以根据具体的条件来选取合适的高斯面，而得到D的值，进一步就可以得到介质中的电场强度E，电极化矢量，以及极化电荷面密度。

最后我们需要了解几个有关电场中的电介质的理论的实际应用，这就是：

电介质的损耗与击穿。

变电体和压电现象。

对于这几种现象，关键是要求我们善于应用理论知识来把握实际问题中的物理图象，也就是善于区分主要因素与次要因素，能抓住复杂现象中的关键过程。

 

电容和电容器。

带电体激发电场，然后电场本身从能量的角度来看，是具备能量的。对于不同的带电体，单位电荷所产生的电场的电势是不同的，这个差别来自于带电体本身的属性，要描述这种属性，我们引入一个物理量—电容。

最简单的是孤立导体的电容，由于是孤立导体，它所激发的电场不受到任何其他的影响，那么它的电势U可以取为相对于无穷远处的电势，如果它所带电量为q那么我们定义它的电容

C=。

可以看出电容这个概念衡量的是导体的一种能力，与它是否带电无关。

注意在国际单位制中，电容的单位法拉并不实用，我们在实际问题中常常是取微法和皮法。

实用的电容总是运用静电屏蔽的原理，使得带电导体所激发的电场不受外界的影响。也即总是设计成把用于储存能量的电场局限在一定的空间里，这样电场的电势就是相对电势，电容的定义就变成了：

C=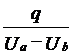

有几种具有典型几何形状的电容器，如平板电容器，球型电容器，圆柱电容器，我们可以通过自己动手进行推导来掌握，而不要死记。

实际上一般的计算电容器的电容的方法并不难，因为电容器的两个极板总是有大小相等，符号相反的电荷，应用公式

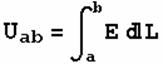
就可以根据定义直接求出电容。

从电介质对电场的电场强度的影响可以知道，在电容器的电场空间充满电介质，可以增大电容量，相比于极板之间为真空的情形，电容量增大的倍数等于电介质的介电常数。

最后，掌握了电容的物理实质，就可以很容易地推导出电容的串联与并联的计算公式。

串联的实质就是把一定大小的总电压分成几份，分别由几个电容器来承受，而每个电容器的电量不变这样在有限电容量的情况下可以提高承受电压的能力。

并联的实质就是使得总的电量可以分配到几个电容器，而每个电容器的电压都不变，这样在一定电压的情况下，总的电量增加了。

最后请同学们根据上述的物理原理，推导出串联与并联的计算公式。尽管简单，但这是一种很好的锻炼，不要忽视。

 

电场的能量。

对于静电场，我们已经分别从作用力的角度（电场强度）和能量的角度（电势）进行了刻划，下面我们总结性地讨论一下电场的能量计算。

我们是从对运动的观测来追溯能量的，在电场中发生的运动只有两种形式，一种情况是电荷在电场力的作用下的运动，这时电场力对电荷作功，同时使得电荷的电势能减少，减少的能量转变为电荷的动能，或者通过电荷的运动转变为别的能量形式。

另一种情况是外力克服电场力对电荷作功，使得电荷的电势能增加，这就使得电场与电荷组成的系统的总能量增加。

根据这样的思路，就可以得到各种情况下计算带电体系或电场的能量的方法。

（1）孤立带电体的能量。

我们可以从电场力的保守性质和孤立带电体的电势能计算公式就可以推导出一个孤立带电体的能量计算公式为：

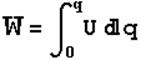
（2）电容器的能量。

电容器从本质上来看就是一个储存能量的器件。它的能量的计算公式类似于孤立带电体的计算方法，它们的物理思路是一致的。差别在于孤立带电体的零点取在无穷远处，而电容器的零点是从两个极板中间选取的。这样可以得到公式：

W=Q²/2C

或者

W=CU²_ab/2=U_abQ/2。

（3）电容器中电场的能量。

上面电容器的能量实际上就是以电场的形式储存着的能量。把公式里描述电容器属性的电容以及极板间的电势差，用描述电场的电场强度和电容器内电场的空间体积，介电常数这些物理量来代替，就得到了计算电容器中电场的能量的公式：

W=εE²V/2

（4）一般电场的能量。

从上面电容器的电场能量的公式和能量体密度的概念，就可以通过积分，推广得到一般电场的能量公式，也就是说，电容器的电场能量的计算公式实际上就是电场单位空间体积内能量的计算公式，通过对整个电场分布的空间进行积分，就可以得到整个电场的能量。

 

    本章的关键概念是电场在空间的可叠加性质。抓住了这个中心概念，就可以处理任何外界对于电场的影响，无非就是电场之间的矢量叠加，而新电场的产生，则是由物性的不同而不同，主要就是分成两类：导体与电介质。这样困难主要就是在于各种不同物质在电场作用下的反应机制。