第十一章.稳恒电流
静电场是电现象最简单的情形,即电场强度的大小与方向在空间各点均保持不变。要得到静电场,一种情况是电荷保持相对静止,本章讨论的是另一种情况,即稳恒电流的情况。
一定数目电子的宏观定向流动。即所谓电流现象。电流是我们日常生活里应用电的主要形式,很多的工作都必须以电流的形式来进行。我们首先考虑最简单的存在于导体内部的,大小不随时间发生变化的恒定的电流,就是所谓稳恒电流。
稳恒电流。
在实际过程中,电荷的宏观定向流动有很多不同的形式:
(1)携带电荷的粒子在宏观物体内部的相对于物体的宏观流动,形成传导电流。
(2)携带电荷的粒子或带电体本身在空间的宏观运动,形成运流电流。
电流的大小有一个直观的度量,就象水流的流量一样,可以定义单位时间内通过导体的电流横截面的电荷的多少,也就是电量的大小为电流强度。
要注意电流是一个标量,我们平常所说的电流强度的方向并不是在矢量的方向的含义上的方向,而只是指在导体内部电场的电力线的方向上,一定的电流是正向还是反向。
对于电流这个物理概念,我们完全可以在大多数的情况下,通过水流的图象来得到直观把握,不过这总是一种比拟,并不是在所有的情况下都是有效的。
完全类似于水流的有关电流的一个基本方程就是稳恒电流的连续性方程。
这个方程的意思就是说在导线的电流横截面上,进入这个横截面的电流一定等于离开它的电流,通过导线中任意两个电流横截面的电流都相等,注意如果存在并行的电流,也就是说导线出现了分支,则需要把并行的分支加起来。
和水流中的质量守恒定律一样,这个方程是电荷守恒定律的直接推论。在直观上是很容易理解的,正因为很直观,同学们往往不能体会到它的重要性。实际上,再复杂的电路中的电流的分析都必须以此为基础。
电流密度。
我们知道在导体中存在稳恒电流,也就意味着在导体内部存在一个静电场,一般认为这个电场局限在导体内部,而且我们一般也只考虑导体内部,这个电场在导体内部的分布是在电场源的作用下,由作为介质的导体本身的分布性质决定的,对于横截面保持不变,材料均匀的导线来说,内部电场的分布是简单而且容易处理的。对于复杂的情形,就需要引入电流密度这个物理量来描述非均匀分布的电场在导线内部每一个空间位置的分布。
我们定义电流密度在导线内部每一点的大小为包含该点的,通过与场强方向垂直的单位面积的电流强度。同时电流密度还是一个矢量,它的方向就是场强的方向。
注意:电流密度的矢量性质来源于电场强度的矢量性质。不能从字面上看,认为密度就是标量。
一段电路的欧姆定律及其微分形式。
稳恒电流既然在实质上就是导线内部的静电场里,电荷以恒定的流量在电场力的作用下作宏观流动,那么产生这个静电场的电势差必定和电流强度有一定的关系。这个关系可以经过实验来得到。
在一般的实验条件下,金属导体满足这么一个很简单的关系,就是所谓欧姆定律:
当导线长度一定时,通过导线的电流强度和导线两端的电势差成正比。
Ua-Ub=I·R。
比例系数表征了导线本身的属性,称为电阻。
注意欧姆定律是有关导线里的电流和导线两端电势差的一条实验定律,它与导线的种类,实验的条件都有关系,有的同学因为常常利用欧姆定律的各种变形来解题,往往忘记了这是一个实验定律。
不过对于一般的金属,在平常的温度下,欧姆定律都是很精确的。
与电阻相关的还有几个概念,首先在很多情况下,我们应用电阻的倒数更为方便,这就是电导。由于电阻反映了导线很多方面的属性,而一般实际使用的导线又是均匀的线材,所以可以尝试消除其中的几何因素。通过实验,我们发现电阻和几何形状的一些关系,对于线材,电阻和长度成正比,和横截面积成反比。然后我们可以把得到的比例系数作为刻划导线电阻中与材料物理属性有关的部分,这样就实际上消除了几何方面的影响。我们把这个比例系数称为电阻率。相应地,它的倒数就是电导率。
欧姆定律所描述的是在一段导体中,电流与电势差的稳恒性质,所涉及的是大块的物质,而我们知道电流的背后是电场,对于电场,我们往往还需要用它在每一点的连续分布来刻划它,那么欧姆定律所对应的微观性质是什么呢?
我们取导线中间任意的体积微元,从关于这个体积微元的欧姆定律就可以推导出所谓的欧姆定律的微分形式:
δ=γE。
其中δ是电流密度矢量,γ是电导率,E是电场强度。
由于在这个关系中,并不涉及到导线与电流在空间上的分布,所以对于非稳恒的情形仍然成立。
电流的功与功率。
我们讨论电场的能量时,已经提到这种能量可以表现为对电荷作功,而电流正是电荷在电场力的作用下的运动,也就是电场力对电荷作功,那么我们可以得到电流的功的表达式:
A=q(Ua-Ub)=It(Ua-Ub)。
那么相应的功率就是:
P=A/t=I(Ua-Ub)。
不过在导线中对电荷作功,必然是电场能量的减少,那么减少的电场能量又转变为什么形式的能量了呢?
有一类现象,就是导线的电流完全由电阻决定,这样当导体通过电流时,得到的唯一后果就是导体发热,这时就意味着电流的功A转变为了热能Q,即:
Q= A
=q(Ua-Ub)
=It(Ua-Ub)
=I2Rt。
这就是所谓焦耳-楞次定律。注意这个定律的适用范围,就是必须是针对一段对于电流而言,完全只是表现为电阻的效应,也就是除了使得导体发热以外,没有任何其他的能量转化过程出现。
另外,我们还有提请同学们注意的是:焦耳-楞次定律是一个实验定律,而不是由别的关系通过推导而来的。更不是能量守恒定律的一个推论,而应该反过来说,焦耳-楞次定律是能量守恒定律的一个重要部分。
我们学习物理,一定要对什么是通过实验而得到的归纳性结论,什么是根据别的基本原理通过逻辑推理而得到的结论有一个清楚的区分。
电动势。
我们至此对于导线中的电流应该已经有了一个清楚的物理图象:就是静电场中电荷的持续流动。
然而我们知道,电荷守恒定律要求当一段导线出现持续不断的电流时,必须还存在一个外部因素,使得正电荷总能补充到导线的电流起始端去。在实际现象中,我们把电路中行使这种功能的部分称为电源。
也就是说,电源所起的作用就是对电荷作功,使得电荷在闭合电路的其他部分能够在电场力的作用下,再把这种电场的能量转变为其他形式的能量。而一般在电源内部,为电荷提供能量的往往不是静电场,对于一种特定的电源总是应用了某种特定的能量形式。
那么我们怎么刻划电源对电荷所作的功呢?引入概念电动势就是为了描述电源提供的这种能力,我们直接定义单位正电荷饶闭合电路一周时,电源对电荷所作的功为电源的电动势:
ε=A/q
我们可以把电源的这种作用类比于电场对电荷的作功,这样和电势相对应的概念称为电动势。我们就可以得到:
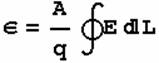
电动势和电势除了场的作用力不同以外,作为刻划场的能量分布的物理量,其他性质都是一样的。即都是标量,并且都最终决定了电荷的电势能。
通过以上的物理分析,我们可以得到一些有用的结论:
(1)在一个闭合电路中,电荷由于电动势的作用而得到的能量等于电场力对电荷作功而消耗的能量。
(2)单位正电荷通过电源时,是从电路的负极到达正极。其所得到的电势能的大小即等于电源的电动势。
(3)单位正电荷通过导线时,是从电路正极到达负极。其所消耗的电势能的大小就等于导线两端的电势。
闭和电路的欧姆定律
在纯电阻电路中加入电源,就得到了一个闭合的能够持续工作的电路。这是所谓闭合有源电路的最简单的例子。
因为电源和电阻电路的主要物理过程是进行了能量的转化,所以首先从能量的角度来分析这样的闭合电路。
这个分析的关键是对电源建立一个虚拟的等效电场过程。由于在闭合电路中处处都要求满足电流的连续性方程,因此不管电源内部实际的物理过程是什么样的,都可以肯定在外部电路存在持续的电流时,在电源内部都存在正电荷的等效电流从电源的负极流动正极,对应这个电源内部的电流,我们同样可以定义与外部导线中的电流相对应的一些物理概念。如电源内电阻,通过电源内电阻的电势降落与增量,最终我们可以得到闭合电路的欧姆定律:
Ua-Ub=ε=I·(R+r)。
其中r为电源的等效内部电阻。注意这个电阻的概念和导线的电阻是完全不同的物理概念,电源的内部电阻只是由电源电动势和闭合电路的电流的比值而得到的一种表观的电阻,并不是说电源内部也存在和导线一样的电阻的作用。
最后,我们必须注意分析闭合电路中的稳恒电流时的一些有关符号方面的约定,常常由于平常不能意识到符号约定的重要性,而在考试中由于把符号约定搞混乱了,而导致许多不必要的错误。特别是当电路复杂起来,包含了多个电源时,更应该注意遵循符号的约定。
在这个基础上,我们就可以得到对于一般的闭合电路的欧姆定律:
I=![]() 。
。
其中的求和,是在进行符号约定以后所得到的代数和。
这样基于对电源的等效图象,得到了最一般的欧姆定律。而严格说来,欧姆定律只是对纯电阻电路有效的,这里进行的推广,是在一种等效的意义上进行的。请同学们记住这里的差别。
金属导电的经典电子论的基本概念。
我们在前面已经成功地应用气体的分子运动论图象很好地解释了气体的宏观现象,那么对于金属导线中的电流这样的宏观现象,是否也可以建立类似的微观图象呢?金属导电的经典电子论就是这样的一种微观图象。
之所以可以把导体内部的电荷类比于气体中的自由运动分子,是因为金属里从晶体点阵里分离出来的电子的运动非常类似于气体分子的自由运动。
这样建立了金属里的电子的气体模型之后,就可以运用气体分子运动论的方法来分析电子运动的宏观效应。
(1)首先我们可以得到所谓电流的电子运动状况,其实是大量自由电子一种定向漂移运动,而并不真正是电子的长距离位移。
(2)可以完全从这个力学图象推导出欧姆定律的微分形式,所得到的电导率的表达式表明电导率分别和单位体积内的自由电子数、电子的平均自由程、电子的热运动平均速率有关,不过这个表达式并不完全精确。
(3)从电子气体的力学图象可以很直观地理解焦耳-楞次热的来源。
最后,作为一个练习,请同学们对上述结论进行推导,在推导时,一定要牢牢把握住电子气体的图象,才能充分运用以前所学过的知识。
电子的逸出功。
最后我们简单地讨论一下电子的逸出功。
本来所谓在导线内传导电流,就是使得驱使电荷运动的电场局限在导体内部,而导体之所以能把电荷局限在其内部,依靠的只能是电场力。我们具体分析一下由于电子热运动而有可能飞出导体时所发生的过程,就会发现有很多因素阻碍电子从导体自由地进入外部,其中一个主要的因素是所谓偶电层,那么电子要飞出导体就必须具备足够的能量。我们把电子为克服电场力拘束而需要作的功称为电子的逸出功。
电子逸出是我们可以应用于很多器件的重要现象。有时我们需要抑制电子的逸出,有时我们需要激发电子的逸出,这都要求我们能够通过某种简单而又足够精确的方式来计算电子的逸出功。
记住一般金属的逸出电势在3到5V之间,对于我们的直观能力是有好处的。
二,疑难。
本章的中心定律就是欧姆定律,对于欧姆定律的理解往往被同学们所忽视,实际上要真正理解这个定律还是有一定难度的,而且常常容易得到错误的概念。
而理解欧姆定律的主要难点在于如何理解它的比例系数问题,也就是说,比例系数为常数是怎么来的?
实际上,我们应该抓住一点,就是欧姆定律本质上是一个实验定律,应该说,它刻画的不是电流通过导线的性质,而是应该反过来说,是通过电流通过一种导线所表现出来的性质,刻画了这种导线的物质属性,也就是说,这个定律实际上是等于定义了一种具有特定的导电性质的导线。进一步,电阻这个概念是和焦耳热紧密联系在一起的。