第十二章.电流的磁场
磁现象的发现并不比电现象晚,但人们一直没有把这两种现象联系起来,而是看成完全不同的相互没有任何关系的两种现象。只是在对于电的研究相当深入以后,才在电流的现象中发现磁的作用,这才提示人们这两种现象的本质关系。
基本磁现象。
最先发现的磁现象是磁铁的相互作用。由于天然存在的磁铁,使得人们非常地熟悉磁铁所表现出来的特性。例如磁铁总是有两个极—南极和北极,同极相排斥,异极相吸引等等,这些特性只有在人们理解了磁性的本性后才能得到解释。
后来又偶然发现了通过电流的导线也具有和磁铁一样的磁性,并且这就一下子大大地扩充了磁现象的丰富性,最终安培提出一切磁现象都来源于电流,而人们熟悉的磁铁这种物质的磁性则是来源于分子的电流。这样就统一了对于磁现象的理解。
磁场。
磁的现象和电的现象具有一个共同的特点,就是相互作用的非接触性。这促使人们提出和电场类似的概念—磁场,以满足人们对于相互作用必须通过接触的顽强直观
那么对于看不见的磁场,我们只有通过它对检验物体的作用来认识它。
通过实验可以发现:磁场的作用首先体现在对于磁场中的磁性物质或者说运动电荷与载流导体产生作用力。而反过来外力作用于载流导体,使得它在一定方向上运动则需要克服磁场力作功。
因此我们首先需要一个物理量来刻划磁场的这种作用力。
磁感应强度。
从实验方便的角度我们首先针对磁场对载流线圈的作用来定义磁场的作用强度。
首先要刻划磁场在空间的分布,那么这个物理量就必须只与磁场中的空间位置有关,而与检验线圈的属性无关,另外对于检验线圈还必须保证对原磁场的作用足够小,而它所感应的磁场区域也必须足够小,从而能近似地表征空间一点的磁场属性。
通过实验可以发现,磁场对于检验线圈的作用表现在对线圈的力矩的作用,因为磁性总是两极同时出现,因此线圈总是表现出两个极性,磁场对它的作用也就必定是力矩的作用。还可以发现磁场的这种作用是有方向性的,因此我们可以通过调整线圈的法线方向,而得到线圈受到最大磁力矩的方向。
回顾我们通过检验电荷来表征电场的电场强度时,是根据电场对检验电荷的作用力来表征的,那个作用力又是与电荷的电流成正比,从而得到作用力与电荷电流的比值,正是表征电场属性的物理量。同样在磁场中,对于线圈的力矩的作用,如果我们取最大力矩的话,可以发现这个最大力矩和线圈的电流以及线圈的面积成正比,而比例系数只是和磁场的空间分布有关,和线圈本身的任何气体性质无关。这样我们定义线圈电流与线圈面积的乘积为表征线圈的属性的一个物理量,称为磁矩,显然这个物理量表征了线圈在一定的磁场中受到力矩作用的性质。由于磁力矩是矢量,因此我们可以相应地规定磁矩的方向为线圈的法线方向。
然后磁矩和最大磁力矩的正比关系使得我们可以定义一个反映磁场本身空间分布的物理量—磁感应强度B。
B=Mm/pm。
磁感应强度的物理意义就是在磁场中,每一点都有一个矢量表征磁场的全部性质,磁感应强度的大小等于单位磁矩的检验线圈在该点所受到的最大磁力矩。而方向则与放置在该点的检验线圈处于平衡状态时的法线方向相同。
请同学们注意我们在寻找刻划磁场的场强物理量时,遵循了在讨论电场时所使用的类似的方法,这不仅是由于电场强度和磁感应强度这两个物理量的类似性,也因为我们讨论场的思想方法的统一性。这是非常值得认真体会的物理思想。
磁力线。
对于磁场我们已经得到了类似于电场强度的刻划场强的物理量—磁感应强度。下一步就可以采取我们在讨论电场时所遵循的途径,来进一步讨论磁场。
首先由于磁场在物理图象上,可以看成在空间的每一点上规定了磁感应强度这个矢量,那么我们可以应用几何的方式,给出一个更为直观的描述,类似于电场的电力线图象,对于磁场也可以定义磁力线。
应用几何语言来描述磁力线,就是磁力线所通过的每一点的磁感应强度的方向就是在该点处磁力线的切线方向。而该点的磁感应强度的大小由在该点取一个与磁感应强度方向垂直的单位面积中所通过的磁力线的数目决定。
记住磁力线的一个重要特征,就是磁力线总是闭合曲线,并且总是和闭合电流相互套合,这个特征深刻地表明了磁场的两极是不可分离的。因此我们称磁场为涡旋场。
另外对于磁场和产生磁场的电流的方向的关系,规定应用右手法则,注意这只是一种约定,并不反映磁场或电流的本质属性。
磁通量。
在磁场的磁力线图象里可以很自然地定义磁通量的概念,即对于任意给定的曲面,通过该曲面的磁力线的数目就是磁通量。我们已经知道通过与磁感应强度垂直的单位面积的磁力线的数目就是面元的磁感应强度,那么磁通量很自然就是磁感应强度在曲面上对面元的积分,写成公式,就是:
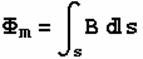
对于闭合曲面,可以得到很重要的关于磁场的高斯定理。
由于磁力线总是闭合曲线,因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来,否则这条磁力线就不会闭合起来了。如果对于一个闭合曲面,定义向外为正法线的指向,则进入曲面的磁通量为负,出来的磁通量为正,那么就可以得到通过一个闭合曲面的总磁通量为0。这个规律类似于电场中的高斯定理,因此也称为高斯定理。
不过我们需要区分这两个高斯定理的重要差别。这个差别就是来源于电场与磁场的本性差别,也就是:
磁场的两极的不刻分离性质和电荷可以单独存在的差别。推出:
磁力线为闭合曲线,而电力线只能始于正电荷,终于负电荷,永远不会自身闭合。推出:
磁场为无源有旋场,而电场为有源无旋场。推出:
磁场的高斯定理和电场的高斯定理的差别。
毕奥-萨伐尔定律。
我们已经能描述磁场了,但要把磁场的起源统一为电流,还需要讨论究竟磁场是如何由电流产生的。
由于在实验中所处理的电流总是通过细长导线的电流,因此下面不妨总是假定电流总是这种形式。
人们发现通过电流的导线对磁针有作用力,那么自然的推导就是:如果磁针所受到的载流导线的作用和受到一个磁场的作用的表现一样,那么可以想象,一定是载流导线也产生了一个磁场,这时在还远远不能了解电磁现象的统一本质的情况下,人们只有通过艰苦的实验,来归纳和总结可能有的规律。最终,毕奥和萨伐尔总结出一条定律,最终解决了任意形状载流导线的磁场分布的问题。
首先磁感应强度是磁场的逐点的局部性质,因此可以想象我们必须首先应用微分形式来表达磁感应强度如何由载流导线的电流以及几何性质决定。
那么载流导线的微分形式必定是某种线元,一方面是几何上的线元,一方面是载有电流的导线,因此我们定义所谓电流元,是线元与电流的乘积,又由于我们前面对电流形式的约定,电流的方向总是沿着细长导线的方向,而导线的方向显然是和磁场方向具有关联性质的,因此还需要取电流元为矢量形式,它的方向就定义为线元中的电流的方向。
然后我们可以很明确地提出问题:考虑一个电流元,求它在空间某一点a所产生的磁感应强度Bi的大小和方向。
进一步的实验表明,a点的磁感应强度Bi和电流元的大小成正比,和a点到电流元之间的距离的平方成反比,还和a点到线元的延伸直线上的最小距离成正比。
而要确定磁感应强度的方向,电流元的方向,电流元和a点到电流元的矢径所组成的平面是决定因素,实验表明,a点的磁感应强度的方向,正是由在电流元和a点到电流元的矢径所组成的平面上的右手系所决定。可以很方便地应用矢量的矢积来表示如下:
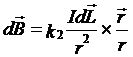
其中k2在国际单位制里表达为μ/4π,而μ为磁场所在的磁介质的磁导率。
对于磁导率我们需要掌握所谓真空磁导率,以及通过和真空磁导率相比得到的相对磁导率的概念,然后对于不同的磁介质就意味着有不同的比例系数表达式。
最后,得到了电流元所决定的磁感应强度的表达式后,在具体问题中,就是求一定长度与形状的载流导线所产生的磁场的磁感应强度的分布。根据磁场的叠加原理,对电流元所产生的磁感应强度进行积分即可。
毕奥-萨伐尔定律最重要的应用,就是求一些在实际应用非常常见的形状的载流导线的磁场分布。如:
(1)直线电流的磁场。
(2)圆形电流的磁场。
(3)载流直螺线管内部的磁场。
对于这些特定磁场的公式不能满足于死记住了,而是要求充分掌握其推导过程的思想,其中最重要的两个步骤,就是对载流导线取典型的线元,然后运用几何对称性进行积分。
无论如何,希望同学们不要只是阅读了教材就了事,一定要自己亲手进行推导,才能载练习中真正掌握毕奥-萨伐尔定律的应用以及这几个特别公式的应用。
磁场强度。
我们继续遵循对电场与磁场进行类比的方式来推进对磁场的研究。
在电场中,实际测量的电场强度是同时由场源的电荷分布和电介质的分布决定的,而电位移矢量在无限大均匀介质中就只由场源的电荷分布决定。同样在磁场中,相似于电场强度的概念就是磁感应强度,而相似于电位移矢量的概念则称为磁场强度。
和电位移矢量一样,要在磁感应强度的概念中消除与磁介质有关的因素,根据毕奥-萨伐尔定律,只需要从磁感应强度的表达式中消去反映磁介质性质的磁导率,就可以得到满足我们要求的磁场强度的概念。即:
H=B/μ
这样一来,磁场的磁场强度就只是和产生磁场的载流导线的传导电流强度,电流依赖导线而产生的分布,以及所讨论的空间位置与导线的相对位置有关。与磁场所在的磁介质没有一点关系。
同样对于磁场强度,可以建立类似于磁力线和磁通量的概念,即所谓磁场线和磁场线通量。只是这时由磁场强度的概念代替磁感应强度的概念来描述磁场的分布。因此可以知道对于同样磁场位置和同样曲面所通过的磁力线通量和磁场线通量,相差μ倍。
安培环路定律。
应用磁场强度的概念,安培得到了一个很重要的定律,就是安培环路定律:
在任意磁场中,磁场强度矢量沿着任意闭合曲线的线积分等于由这个闭合曲线所包围的所有传导电流的代数和。
安培环路定律中电流的正负方向和线积分的方向是根据右手法则确定的。
可以得到一个很简单的推论:
如果在闭合曲线内包含等值反向的电流,则磁场强度的线积分为0。
安培环路定律最主要的应用是计算具有一定对称性的电流分布所产生的磁场强度。这里我们必须注意应用安培环路定律的条件:(1)只能计算闭合电路所产生的总磁场强度。(2)要求电流分布具有一定的对称性。
而在实际问题中应用安培环路定律的关键是如何选取恰当的积分曲线。首先这条曲线必须通过我们要讨论的一些典型点,然后再尽量使得要选取的曲线能够使B作为常数。有两个技巧,就是在曲线上使得B的方向总是与曲线相切,而B的大小不变;或者如果只有曲线的一部分具备上述特征,则尽量使得其余部分的B为0,或与曲线垂直。
最后,请熟练掌握三种电流分布的磁场强度计算方法,而不只是公式:
(1)
长螺线管内部。
(2)
环形螺线管内部。
(3)
无限长载流圆柱导体的内外部分。
运动电荷所产生的磁场。
我们讨论了电流所产生的磁场,而电流实质上就是电荷的一种运动,因此我们要讨论运动电荷产生磁场的性质,就是从微观的角度来分析毕奥-萨伐尔定律。
在毕奥-萨伐尔定律的推导中,最为关键的是使用了电流元的概念,而如果具体地把电流元中的电流看成一定数目电荷的定向运动,那么就可以把毕奥-萨伐尔定律里的宏观物理量—电流,代替为微观上的物理量-电荷的电量,电荷的运动速度。最后得到对于运动电荷的“毕奥-萨伐尔定律”:
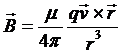
二,疑难。
磁感应强度与磁场强度的区别在哪里?
[答]:这两个概念的关系完全类似于电场强度和电位移这两个概念的关系。
从定义的操作方面来看,磁感应强度是完全只是考虑磁场对于电流元的作用,而不考虑这种作用是否受到磁场空间所在的介质的影响,这样磁感应强度就是同时由磁场的产生源与磁场空间所充满的介质来决定的。相反,磁场强度则完全只是反映磁场来源的属性,与磁介质没有关系。这两个概念各有其方便之处,我们应该同等地重视。