第十四章.电磁感应
回顾一下我们已经学习过的知识。
首先我们研究的物理对象是静电场,然后研究了在静电场里作定向运动的电荷,就是所谓电流,在仔细分析了磁现象的规律后,我们把磁场归结为是电流所产生的。这样就有了对于由电流所产生的磁场的研究,由于磁场之间的相互作用,相应地就会发生磁场对载流导线的作用。进一步,我们现在还要研究磁场产生电流的效应,从而更深刻地了解电与磁之间的关系。
电磁感应的基本定律。
这里最关键的发现是法拉第得到的。应该说正是这样的实验事实促使人们发现了电与磁之间的深刻统一性,而不是先有某种统一性的观念启发人们去找到实验现象。
法拉第发现的现象是:如果通过一个闭合回路所包围的面积的磁感应强度通量发生变化,闭合回路中就会产生电流。
这个电流就是感应电流。楞次进一步通过总结实验得到感应电流方向是如何决定的物理原因,即闭合回路中的感应电流所产生的磁场,总是要补偿或反抗导致感应电流的原来的磁场的磁感应强度通量的变化。这就是楞次定律。
最后法拉第总结出决定感应电动势的关系式,即法拉第定律:
磁场中的闭合回路里所产生的感应电动势与通过回路面积的磁通量对时间的变化率成正比。
即
注意其中的负号,一定不能忘记,因为所谓楞次定律就是反映在这个负号上面。另外我们还可以应用右手法则来反映楞次定律,因为所谓右手法则无非就是一种固定的标定三维空间的三个方向的方法,由于产生感应电流的过程中涉及到三个方向:闭合回路平面的电流环绕方向(两个维度)和磁通量的方向,这三个方向的相互关系是唯一确定的,因此只要对应好两个方向,就可以唯一确定第三个方向。在这里,就是规定好一个回路环绕的正方向,就可以由磁通量的变化率的正负来决定电流在那个方向上的正负,请同学们认真体会一下这里的技巧,这种技巧在物理学中是非常常见的,也是非常有助于我们作题时不至于把符号和方向搞错。
由于电动势和磁通量的时间变化率的量纲一致,因此比例系数可以通过取适当的单位而为1。
进一步,如果假设闭合回路是纯电阻电路,就可以计算感应电流和一定时间内通过回路一个截面的感应电量。
特别的,由于感应电量和感应电流相比,没有时间变化的因素,得到的感应电量与磁通量的时间变化率没有关系,而是和磁通量的变化值成正比,这可以应用于磁通量的测量。
如果闭合回路是由多匝线圈组成,则总的感应电动势就是各个单匝线圈的感应电动势的总和。
磁场中运动的导线内的感应电动势。在磁场中转动的线圈内的感应电动势和感应电流
历史上开始发现的是闭合回路中的感应电流,是因为电流便于测量,实际上,对于非闭合的回路,也存在磁通量发生变化的情况,这时在回路里就不会产生感应电流,但会产生感应电动势,因此在刻画电磁的感应现象时,更本质的物理量是感应电动势。
我们再讨论两种磁通量发生变化的情况。
(一)在静磁场中的运动导线。
我们在分析磁场力对载流导线作功时,已经建立导线切割磁力线这种直观图象,而切割磁力线实际上也是一种磁通量的变化,因此相应的对于磁场中的运动导线,在切割磁力线时,同样产生感应电动势,
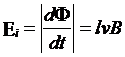
其中l为在垂直于B的平面上切割磁力线的直导线的长度,v为导线平动的速度。
这个现象完全可以应用洛仑兹力的概念和金属电子理论来进行解释。但不能应用它们来解释闭合回路由于通过回路面积的磁通量变化而产生感应电动势的现象。这时需要引入新的概念,我们在后面根据麦克斯韦的理论来讨论。
(二)在静磁场中转动的线圈。
在静磁场中转动的线圈自然会发生通过线圈的磁通量的变化,对于匀速转动,这种变化与时间成正弦函数关系,这样就得到一个与时间成正弦函数关系的感应电动势和感应电流,这就是交流电的产生。
对于N匝面积为S的线圈,角速度保持为ω,则感应电动势为
Εi=NBSsinωt
感应电流为
I=I0sin(ωt-θ)
其中I0为最大电流强度,θ为电流落后于电动势的相位差。
涡旋电场。
迄今为止,我们讨论的电磁现象还都不能离开电荷而单独存在,都需要电荷的参与。静电场固然需要由电荷激发,磁场更是由电流产生的。磁场产生电流也试图归结为磁场对运动电荷的作用力—洛仑兹力,但我们在上面已经讨论过,对于固定闭合线圈,由于通过线圈面积的磁通量的变化而产生感应电动势,是不能由洛仑兹力来解释的。
这里为了进一步发展物理学,麦克斯韦表现了极大的洞察力,他认为电场和电荷一样,应该具有同样的实在性质,因此他从这样一个观念出发,认为变化的磁场能产生单独的电场,而无论是否有电荷的存在,这种电场的存在,正好由在变化的磁场中的闭合回路里产生了感应电流而表现出来,也就是说,变化的磁场总是能产生电场,一旦在这个电场中的合适位置上放置了一个闭合回路,就会在这个回路中导致自由电荷的运动,即形成电流。
但是这种由磁场所产生的电场与静电场完全不同,静电场是有源无旋场,表现为电力线总是起始于正电荷,终于负电荷。而这种电场的电力线却是闭合曲线。这种电场被称为涡旋电场。
把通过法拉第电磁感应定律所得到的感应电动势理解为在涡旋电场中对回路电荷作功而得到的能量变化,麦克斯韦就得到了涡旋电场与变化磁场的关系:
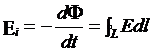
从这个公式还可以看到涡旋电场和静电场的一个终于区别:静电场的环流为0,而涡旋电场的环流为回路内磁通量的时间变化率的负值,这表明涡旋电场不是保守力场。
涡旋电场有一个重要应用就是电子感应加速器。
涡电流。
如果把线圈换成整块的金属,就会出现涡电流的现象。实际上,整块金属和线圈的区别就只是电流端面和长度的比例而已,如果把整块金属看成多匝线圈的叠合,自然就会得到涡电流。
研究涡电流的目的一是由于可以利用这种现象,另外是由于在一些场合需要避免这种现象的发生。
自感应。
对于闭合回路线圈,如果我们不是考虑它的外部磁场对它的影响,而是让线圈本身通过电流,那么这个电流本身也能产生磁场,如果这个磁场通过回路的磁通量也发生变化,那么就同样会产生感应电动势,这个感应电动势称为自感电动势。
根据毕奥-萨伐尔定律,我们可以由线圈中的电流,得到其所产生的磁场的磁感应强度的分布,电流强度与任一点的磁感应强度成正比,也就是说与通过回路的磁通量成正比:
Φ=LI
其中比例常数L称为自感系数。从毕奥-萨伐尔定律可以知道自感系数与磁介质的磁导率以及线圈的几何性质有关。
再由这个磁场在线圈里产生感应电动势,根据法拉第电磁感应定律可以得到自感电动势为
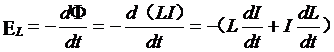
注意负号反映了线圈的某种“电磁惯性”。
互感应。
如果两个载流回路在空间上位置邻近,从而每个线圈所产生的磁场都能影响另一个线圈,并当这个磁场发生变化时,使得另一个线圈产生感应电动势,这个现象称为互感应。所产生的感应电动势称为互感电动势。
不考虑两个线圈的相互位置发生变化和周围磁介质的磁导率发生变化的情形,这样产生感应电动势的原因就只是通过线圈的电流的变化。
类似于自感应现象,可以分别得到两个线圈里由于另一个线圈电流变化导致磁通量变化而产生的感应电动势。同样在上面的条件下,可以得到互感电动势与激发电流的时间变化率成正比,比例系数称为互感系数,处理方法和自感的情形一样,只是这里是两个线圈发生相互作用。
磁场能量。
磁场能量可以通过自感现象表现出来,在自感过程中,由于自感电动势的产生,或者使得回路中的电源需要为克服自感电动势而作功,或者回路电流得到自感电流的补偿而增加了热能,这里都是以磁场作为了能量的一种储存形式。
可以一般地得到磁场能量体密度为
wm=BH/2=μH2/2
其中μ为磁场空间的磁介质的磁导率。
这样对于一般的磁场,取磁场空间的体积元,得到体积元的磁能,然后再在整个磁场空间进行积分就可以得到整个磁场的能量。
二,答疑解难。
(一)本章的中心内容就是磁生电。这里的关键就是磁生电的条件是什么。
如果按照对实验现象的归纳来描述这个条件,就回显得非常没有条理,只有把所有的现象都归结到一个概念上面,即磁通量的变化,就可以完备地给出条件的描述。
那么磁通量的变化实际上是可以通过许多途径来得到。
首先就是B本身的变化,当然导致磁通量的变化,第二就是所考虑的载流回路的面积的变化,第三就是所考虑载流平面与B的夹角的变化,这三种因素可以只有一种,也可以同时有多种发生作用,这就需要我们在实际问题中仔细分析与判断的了。
第二个初学者常常容易犯错的地方就是在磁生电的现象中的几个方向之间的关系问题。
在感应电流的产生过程当中,回路平面上的电流环绕方向与磁通量方向构成右手法则,反映在楞次定律里面,就是那个负号,初学者常常在这里犯错。
最后,初学者往往不能体会到电磁感应现象里面的主宰,实际上就是能量守恒定律。只有能够体会到能量守恒定律是如何体现在电磁感应现象里面的,特别是如何通过楞次定律鲜明表达出来的,就可以彻底地掌握电磁感应的规律。
(二)本章还涉及到了一些比较抽象而微妙的概念。
首先是感生电动势与动生电动势的区别。它们的区别实际上就是来源于上述磁通量变化的不同方式。尽管非常容易理解,但在实际问题中,有时候需要我们分别讨论这两种电动势,而从理论方面来考虑,则涉及到一个重要的而且是非常抽象的概念,就是涡旋电场的概念。因为要解释感生电动势只有依靠涡旋电场的概念。