第十七章.光的干涉
光源。光的单色性和相干性。
光源的发光机制一般是相当复杂的，不过发光终究是由于分子或原子的能态被外界能量激发而吸收能量以后，再从高能态返回低能态而放出能量的过程。
对于热光源来说，分子或原子的激发是通过热碰撞而实现的，然后再间歇地辐射出电磁波来，一般这种激发与辐射过程是相当参错不齐的，只满足某些统计性的分布规律。因此一般的光源所发出的光总是具有一定的频宽。
如果我们为了在比较简单的情况下来研究光，常常需要单色光，也就是具有一个确定频率的光束，一般使用的方法，首先是尽量选择单色性比较好的光源，也就是频宽比较窄的光源，然后再应用色散来选择所需要的频率的光。
光的相干现象本质上是来源于波动的叠加性，要希望观察到光波的空间干涉现象，首先要求是单色光，以光波的电场强度分量为例，只要画出单色光的E的空间分布图形，就可以发现两列波在空间重叠而发生相干的必要前提是：
（1）频率相同
（2）振动方向相同。
（3）周相相同，或周相差保持不变。
显然一般光源在下列情况下所发出的光都是无法满足这个条件的：
（1） 两个不同光源所发出的光；
（2） 同一个光源的不同部分所发出的光。
（3） 同一个光源的同一个部分（甚至同一个原子）在不是同一个时刻所发出的光。
获得相干光的方法。
在激光出现以前，人们为了要获得相干光，主要的思路是选择尽量细的一束光，使得它的来源尽量保证在光源的同一个部分，然后把这一束光分成两束，再使这两束光在空间重叠而发生相干现象。
我们需要了解三种依据这种思路而获得相干光的方法：
（一）杨氏双缝。
（二）菲涅耳双镜。
（三）洛埃镜。
这三种方法的共同特点就是尽量做到把一束光的同一个波阵面分成两束光来。
产生干涉明暗条纹的条件。
根据光的波动图象，可以很好地分析干涉现象。我们可以应用波动图象计算双缝干涉中观察到的明暗条纹的分布与波长以及干涉中的几何尺寸的关系，从中可以看出对这两束光必须要求什么样的条件才能满意地观察到干涉条纹。
如图所示：
设在一个时刻到达两个小孔的是同一个波阵面，根据惠更斯原理，在每一个小孔处都可以看成是一个波源，这两个波源所发出的波由于是属于同一个波阵面，所以它们的频率相同，振动方向相同，周相也相同，是属于相干光。
如果我们如图所示在屏上任取一点P，这一点距离屏上与两个小孔等距的点为x，而两个小孔发出的光要到达屏上的这一点，必须分别经过r1，r2的距离。那么屏上x处的的干涉条纹分布情况如何呢？
我们只考虑条纹上的两种位置，即最亮的和最暗的位置。也就是说我们要求x满足什么条件时为最亮的和最暗的位置。
两束相干光到达P时，波程差
I= r2 -r1
可以得到波程差和周相差与波长的关系，根据干涉条件，周相差必须为π的偶整数倍，P点才是最亮的，周相差必须为π的奇整数倍，P点才是最暗的，由此可以分别推出波程差必须满足的与波长的关系。
然后从图中的几何关系，为了得到比较简单的关系式，我们取r2 +r1=2D，这就要求D远大于2l，从而得到当
x=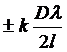
，k=0，1，2，···
时，P点最亮。当
x=
，k=0，1，2，···
时，P点最暗。
应用类似的方法，我们可以分析其他两种相干方法。不过对于应用镜面反射来使得两束相干光在空间重叠的那两种方法，出现了所谓半波损失的现象，也就是光线通过镜面反射后，在光线的路程上必须减去半个波长，这点通过洛埃镜的实验可以得到验证。
光程和光程差。
从上面我们对于干涉的分析，可以知道发生干涉的关键在于两列光的周相的匹配，直观地说，就是两列光的波的形状在同一时刻到达同一地点的配合。而我们知道一般的相干现象里，两束光线发生相干时，并不是发生在同一个波阵面上，而往往是不同波阵面上的相干光在同一时刻重叠于同一地点。这样周相差就是关键的决定相干的物理量。在上面的例子里，我们通过计算两束光线的空间路程差得到了它们的周相差。
那么当光线行进过程中通过了不同的媒质时，由于光的传播在不同媒质里的频率保持不变，而速度比在真空中要减慢，因此相应的波长也就减小，即真空的波长除以媒质折射率。反过来这就意味着，当光在折射率为n的媒质里行进的几何路程为x时，在相同时间内相同的波数所行进的路程为nx，那么我们就把光在通过任意媒质时的传播路程，都折算为在真空里的传播路程，这样在比较通过了不同媒质的两束光时，就能直接得到周相差，因为在这种情况下，周相差不能通过两束光的空间上的路程差直接得到。
因此我们为了方便分析两束通过不同分布的传播媒质的光线的相干，就引入所谓光程的概念。就是把光在某种媒质中传播的空间路程，通过乘以媒质的折射率，折算为光在相同时间内相同的波数在真空里的传播路程，就是它的光程。
那么周相差就可以直接由光程差得到：
周相差=2π·光程差/光在真空中的波长。
这样应用光程差的概念，我们就能很方便地分析光通过不同的媒质时所发生的相干现象。下面我们还要分析三种这样的干涉现象。
而且应用光程差的概念，我们也可以用来理解很多光的传播过程的性质。例如分析光通过透镜的过程，可以知道透镜对光线的作用只是改变它的空间路径，而不会改变它的光程，因此通过透镜能得到物体的实象。
薄膜的干涉。
分析等厚薄膜的干涉必须注意以下几点：
（1）
薄膜干涉是面光源所发出的光线的干涉。
（2）
通过薄膜观察到干涉现象有反射与透射两种情况。
（3）
反射的情形是由同一点光源发出的光线，分别经过在薄膜上表面反射和在薄膜下表面反射，通过了不同的媒质路径，最后到达眼睛时，产生了光程差，从而出现干涉条纹或彩色条纹。
（4）
注意两束光线的反射，分别是从光疏媒质到光密媒质的反射，和从光密媒质到光疏媒质的反射，从光疏媒质到光密媒质的反射会出现半个波长的光程差，就是所谓的半波损失，反之，则不会。
（5）
透射的情形是一束光直接透射，而另一束光经过连续的媒质内部反射后再透射出来的，计算着两束光的光程差，必须注意在媒质内部反射的光线不存在半波损失。
（6）
这种通过不同媒质间的反射，折射与透射而得到的相干光，是利用分振幅的方法而得到的。
劈尖的干涉。牛顿环。
（1）
劈尖与牛顿环的干涉现象都是属于非等厚薄膜上发生的干涉。
（2）
劈尖的干涉是由分别在劈尖的上下两个表面上反射的光线所形成的，入射光线垂直于劈尖上表面。每一个干涉条纹都对应于一个确定的劈尖厚度，这种干涉条纹倍称为等厚干涉条纹，因此劈尖干涉现象可以用来检验媒质表面的平整程度。当上下表面的媒质完全平整时，得到的是疏密均匀的平行直线形的干涉条纹。否则就是疏密不均匀的曲线条纹。
（3）
牛顿环的干涉是由分别在透镜下表面和平面玻璃上表面所反射的光束所产生的。得到的干涉条纹也是等厚干涉条纹。为以接触点为圆心的同心环，接触点为暗点。
迈克耳孙干涉仪。干涉现象的应用。
迈克耳孙干涉仪有几个关键的地方需要注意：
（1）
迈克耳孙干涉仪的设计思想，主要是应用两块完全反射镜，和一块半透半反镜，两块完全反射镜的反射平面相互垂直，半反半透镜以45度夹角放置在两块完全反射镜的法线交点位置上，这样可以通过由半反半透镜对一束光进行分光，分别由完全反射镜反射回来，再一次通过半反半透镜，使得两束光产生干涉。
（2）
迈克耳孙干涉仪综合应用了两种干涉现象，即等厚干涉条纹与等倾干涉条纹，两个完全反射镜面如果不是严格垂直，光线所经过的路程中就相当于出现了空气劈尖，从而干涉得到平行的等厚条纹；如果两个完全反射镜面严格垂直，就相当于等倾干涉，从而出现等倾干涉条纹。
（3）
干涉条纹在屏上的位置取决于光程差，所以通过调节一块完全反射镜的位置，就可以观察到条纹的移动，条纹本身是一种宏观的图象，而条纹移动一条，就对应于反射镜移动了半个波长，视场中明纹移动的数目m与反射镜移动的距离d的关系是：
d=λm/2
其中λ为光的波长。
因此迈克耳孙干涉仪的实在功能就在于放大了微观距离。
（4）
应用迈克耳孙干涉仪的这种功能，我们可以利用已知的光的波长来测量精确度要求很高的长度，或者反过来，利用已知的长度来测量未知的光的波长。历史上，迈克耳孙应用它定义长度的单位—米。
从迈克耳孙干涉仪的原理可以看出利用干涉原理可以进行微观空间位移的测量，而很多的物理测量中，都涉及到微观位移的测量，因此干涉现象可以由极其广泛的应用。
在应用迈克耳孙干涉仪时，还会发现一个问题，就是所谓相干长度的问题。
这个问题的起源是光源发出的光波不是连续的，而是离散的波列，这样当到达相干空间区域的两束光线的光程差超过了波列长度，就使得相干性不再被满足。要刻划单色光源的相干性程度，我们定义这两束光能产生相干的最大光程差为相干长度，相应的时间称为相干时间。
实际上，在应用迈克耳孙干涉仪产生干涉现象时，还存在一个问题，就是光源的单色性问题。一般的所谓单色光其实是围绕一个中心频率的有一定宽度的频率分布的光，谱线宽度是波列持续时间的倒数，而波列持续时间就是相干时间，由此可以得到相干长度和谱线宽度成反比，因此所谓光源的单色性好，就是相干长度长。
二，疑难。
光速具有有限值是发生相干的一个必要条件，因为如果光速是无限的话，就不会存在相位的概念，自然也就不会出现作为典型的波动现象的干涉。