第十八章.光的衍射
历史上，除了干涉现象以外，还有一种现象有力地表明了光的波动属性，这就是衍射现象。
光的衍射。
衍射的实质还是一种干涉。这种干涉的发生在现象上表现为光线遇到与波尺度相比拟的障碍物时，出现直线传播的发散与展衍现象。
一般我们观察衍射现象，是让光通过一个透光孔，形状可以是圆孔，或狭缝，当透光孔的尺度小到可以和光的波长相比拟时，光通过透光孔厚到达一个屏幕上，就可以观察到衍射条纹。
衍射分成两种：
（1）
菲涅耳衍射：
透光孔与光源和屏幕的距离总有一个是有限远。
（2）
夫琅和费衍射：
透光孔和光源与屏幕的距离都是无限远。因此是通过透镜得到平行光而进行衍射的。
惠更斯-菲涅耳原理。
惠更斯已经指出光波传播的一个基本图象，就是光波在媒质中所到达的任意点，均可作为子波的波源，在后面的任何时刻，这些子波的包迹决定了在那个时刻的波阵面。
进一步，菲涅耳指出，由同一个波阵面上各个点所发出的子波，在空间相遇，则会通过叠加而发生干涉现象。
这两个结论加起来就是惠更斯-菲涅耳原理。
这个原理可以一般地解释很多波动现象，但从原理的表叙可以知道，应用惠更斯-菲涅耳原理来计算波动过程，实际上就是对波阵面上的每一点进行积分，这在数学上是极其复杂的，我们不作要求。
通过这个原理可以很好地通过干涉来解释衍射现象。下面我们就是主要应用这个原理来解释一些衍射现象。
单缝和圆孔的夫琅和费衍射。
要一般地运用惠更斯-菲涅耳原理来计算衍射过程，需要进行繁复的积分运算。因此我们使用一种直观的方式来理解夫琅和费衍射，就是所谓菲涅耳波带法。
首先考虑单缝夫琅和费衍射。
从惠更斯-菲涅耳原理的观点来看，衍射的关键是透光孔限制了一个波阵面，使得这个部分波阵面的各个点所发出的子波相互干涉而出现衍射图样。
（1）
在任一个时刻到达单缝的是一个波阵面，单缝的足够小的尺寸保证了这点，而单缝本身的阻碍作用又使得只有部分波阵面参与了衍射。
（2）
到达单缝的光线是相互平行并且垂直于单缝面。
（3）
注意一个关键的地方就是从单缝处的波阵面上，每一点所发出的子波，叠加在一起，可以用另一个观点来看，就是宽度为单缝宽度的一束一束的平行光，这些平行光束由于完全是由单缝处波阵面的子波组成，因此必然会从原来平行光的方向会有一定范围的连续的偏离，对于任一束平行光，偏离的角度称为衍射角。
（4）
单缝后面放置的透镜保证从单缝波阵面的任意点上所发出的子波的任意方向的平行光束，都聚焦在屏幕的一点上。
（5）
考虑屏幕上的一点，是由单缝波阵面上每一点所发出子波中具有相同偏离方向的一束光线所聚焦或者说叠加而成。
（6）
对于一束具有相同偏离角的光线，取一系列相互平行的平面，垂直于光线行进方向，在单缝面处，这一系列平面把起始波阵面划分为一系列与单缝边平行的长条带。这就是所谓菲涅耳波带。
（7）
规定平行平面的相互距离为入射光的波长的一半，那么相邻的波带上任何两个对应点的光程差都是波长的一半。
（8）
由于透镜本身不影响光程，所以任意相邻的两个波带所发出的光线都一一对应的相互干涉抵消了。最终如果这一束光的单缝最上沿的光线与最下沿的光线的光程差为半波长的偶数倍时，那么屏幕上的相应点处就是暗的；最终如果这一束光的单缝最上沿的光线与最下沿的光线的光程差为半波长的奇数倍时，那么屏幕上的相应点处就是亮的。
（9）
最后我们就能得到衍射角与屏幕上的条纹的对应关系：
设衍射角为w，单缝宽度为a，波长为l，那么当
-l<asinw<l
得到中央明区。
满足sinw=l/a的衍射角，称为半角宽度，可以得到半角宽度大约等于波长除以单缝宽度。
当asinw=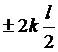
，k=1，2，3，···时，得到屏幕上的暗条纹。
当asinw=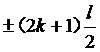
，k=1，2，3，···时，得到屏幕上的亮条纹。
可以看到单缝宽度的决定性作用，在宽度大于或等于波长时，就会出现明显的衍射图样，在宽度远大于波长时，则各级衍射条纹重叠在一起，从而不会出现衍射图样。
由于光学仪器中所使用的透镜一半都是圆形，所以常常使用小圆孔代替长条单缝，这就是圆孔夫琅和费衍射。
圆孔夫琅和费衍射和单缝夫琅和费衍射本质上是一样的，只是形成的衍射图样不同，中央明区对应的是中央光斑，称为爱里斑，占整个入射光束总光强的84%。
类似的圆孔夫琅和费衍射的半角宽度大约等于波长除以圆孔直径，只是还有一个系数1.22，反映了几何上的差异。
衍射光栅。
如果把大量宽度一样的单缝相互平行等距地排在一个平面板上，就是光栅。单缝宽度和缝间距之和称为光栅常数，表示光栅的精细程度。
垂直通过光栅的平行光，首先是通过每一条单缝发生单缝衍射，然后通过每一条单缝的光线再发生干涉，最终在屏幕上得到总的效果。
按照我们以前对单缝衍射的分析，平行光从单缝出发，以某个角度（衍射角）到达透镜的一束平行子波，会聚集在屏幕的一点上，在一定条件下，这个点构成明条纹里的一点，而由于光栅是大量的单缝平行等距排在一贯平面上，所以每个单缝发出的相同衍射角的子波光线都聚集在同一点上，因此每一条明条纹的光强都是所有单缝的贡献的总和。
衍射角满足如下条件，即所谓光栅公式：
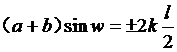，k=0，1，2，3···其中a+b为光栅常数，w为衍射角，l为波长，k表示明条纹的级数。
就形成最亮的明条纹，称为主极大条纹，不过其中有一部分衍射角，同时满足条件：
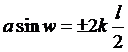，k=1，2，3···
则在通过单缝时已经是暗条纹了，因此不会在屏幕上形成明条纹，这种现象称为缺级现象。
其他衍射角则更容易形成暗条纹。
从以上分析可以得到：
（1）
光栅常数越小，各级明条纹分开越明显。
（2）
光栅的狭缝越多，透射光束越强，明条纹越亮。
因此应用衍射图样来测量光的波长时，光栅比单缝更好。
光栅的另一个重要应用可以从光栅公式看出来，即在光栅常数确定的情况下，衍射角与波长有简单的关系，可以想象，非单色光通过光栅所形成的光谱就是按照简单的光栅公式分布的。这种光谱与棱镜所形成的光谱相比，具有分布简单的优点。因此在光谱分析时，常常应用光栅所形成的衍射光谱
光学仪器的分辨率。
由于衍射现象的存在，使得光学仪器的分辨率是有限的。
光学仪器的最大分辨率可以通过使用所谓瑞利分辨判据来定义：
一个点光源通过一个光学仪器所形成的衍射图样的中央最亮处，如果刚好和另一个点光源的衍射图样的第一个最暗处重合，则称这个光学仪器刚好分辨了这两个点光源。这时两个点光源在透镜处所张的角度称为这个光学仪器的最小分辨角，而最小分辨角的倒数则称为这个光学仪器的分辨率。
如果以发生了圆孔夫琅和费衍射的一般光学仪器为例，可以从第一极小用波长和圆孔直径表示的公式看出：
（1）
光学仪器的分辨率与其孔径成正比；
（2）
光学仪器的分辨率与所使用的光的波长成反比。
伦琴射线的衍射。布拉格公式。
伦琴射线就是所谓X射线，波长比一般可见光要小，因此要用X射线来做光栅衍射，只有使用某种天然而特别的光栅—晶体。
应用晶体作为光栅进行衍射时，有两种方式：
（1）
劳厄所使用的射线透过晶体，在胶片上形成衍射斑点，即劳厄斑点。
（2）
布拉格把晶体看成由平行晶面构成，用X射线以小角度w掠射到晶体表面，受到晶体表层与内部各层的散射，其中完全反射的部分强度最大，并且在满足如下条件（即所谓布拉格公式）时：
2dsinw=kl， k=1，2，3，···（其中d为晶体的晶面之间的距离，即晶格常数，l为X射线的波长）。
各个反射线都会相互加强，从而形成亮点。
利用晶体作为X射线的衍射光栅具有极为重要的应用价值，一方面如果已知一种晶体的晶格常数，应用这种晶体作为光栅就可以测量某种来源X射线的波长，这被用来分析原子结构；另一方面，应用已知波长X射线，以某种晶体为光栅，通过衍射图样来分析这种晶体的结构，这种应用在今天研究各种分子晶体，特别是生物大分子晶体的结构，发挥了极其重要的作用。
二，疑难。
发生衍射现象的关键是单缝的宽度，而决定衍射条纹的是在单缝的上下边缘处的波振面位置所发射的子波。