第二十一章.光的量子性

人类遭遇物质的量子性质，一个地点就是热辐射。在电磁理论比较成熟以后，人们把对电磁现象的研究领域扩展到了一般电流与可见光的范围之外，由于工业上的金属冶炼的需要，物质因热而发光乃至发射辐射能，开始成为人们研究的对象。恰好是在分析一些热辐射规律的产生原因时，人们被迫引入了辐射或光的量子性质。

 

热辐射。

物质在原子层次的电磁结构以及不停息的分子热运动，导致物质总是在发射电磁辐射，这种辐射的强度和频率分布是随物体温度而发生变化的，因此称为热辐射。

热辐射的一个重要特征就是按照频率或波长存在一定的分布，而实验表明，这种分布与温度，物质的材料，甚至物质的表面情况都有关系。为了更具体地研究热辐射在不同波长时的辐射强度分布，我们引入物理量—单色辐出度，用来表示从物体表面单位面积发出的，波长在一个确定小范围内的辐射的功率。

而在物体表面，用单色辐出度对辐射所涉及的整个波长范围进行积分，就得到物体表面单位面积的所有波长的总辐射功率。称为物体的辐射出射度。显然辐射出射度是比单色辐出度更为粗略的概念，它只与温度有关。但它表达的也还是材料的已知属性。

基于同样的理由，外界的电磁辐射也能对物质的电磁结构发生作用，也就是说物质在发射电磁辐射的同时，也能吸收和反射电磁辐射。最简单的描述物质的对电磁辐射的吸收与反射的方式就是直接定义吸收的辐射的能量占总入射的能量的比例为物体的吸收比。反射的电磁辐射的能量占总入射辐射能量的比例为物体的反射比。这样在没有透射的情况下，在一定的情况下这两个比值的和为1。

更精细地分析这两个比值，通过实验发现它们都和物体的温度与入射辐射能的波长有关系，因此更精细地使用这两个概念的方式是把它们看成温度与入射辐射能的波长的函数。

 

绝对黑体。

为了更进一步地研究物质与辐射的相互作用，有必要构造一种比较简单的理想模型，那就是由于辐射的反射，并不是有太大的研究价值，因此我们希望首先研究一种物质，在和辐射发生相互作用时，可以完全不考虑它对辐射的反射作用，从而能比较单纯地分析物质与辐射的相互作用，这样的理想模型就是绝对黑体。根据我们的要求，显然它的吸收比在任何温度以及对任何波长的辐射都是1。

这样的物质在自然界显然是不存在的，但是还是能找到在一定条件下与绝对黑体近似的真实物质系统。最常用的系统就是有绝热壁构成的一个空心容器，器壁上有一个小孔，小孔的尺度远小于容器的尺度。因此所谓这个黑体吸收辐射，就是有辐射从这个小孔进入容器内部，注意，容器是由绝热壁构成，因此热辐射无法直接通过照射在器壁上被容器吸收。那么尽管容器的内壁的吸收比无法作到是1，但辐射进入容器后，不能被吸收的部分继续被容器内壁反射，而每反射一次，就会根据吸收比被吸收一部分，这样如果容器内壁的吸收比为α，入射的总能量为1，则经过n次反射以后，剩下未被吸收的能量就只有（1-α）ⁿ了。

反过来考虑这个绝对黑体所发射的辐射，显然也只有从小孔射出的辐射才是这个绝对黑体的在小孔的大小那样的面积上所发射的辐射。

 

基尔霍夫定律。

从直观上看，物质处在一定的辐射环境中时，同时在吸收辐射能与发射辐射能，只要物质是处于一种平衡状态，它吸收与发射的辐射能应该保持一种平衡，否则不是物质内部所含的能量不断增加，就是不断减少，显然这不符合我们的日常观察。

基尔霍夫从理论上给出了我们的以上直观认识，就是发现物质的单色辐出度与吸收比的比值是一个常数。这个常数与物质性质无关，而只和温度与辐射能的波长有关。

进一步，考虑到绝对黑体的吸收比为1，既然这个常数与物质的具体性质无关，那么它代表了一般的辐射相互作用的性质，因此我们可以把这个常数，归结到绝对黑体上来，以便于进一步研究，这就表叙为基尔霍夫定律：

在一定温度下，任何物质的单色辐出度和单色吸收比的比值，等于同样温度下的绝对黑体的单色辐出度。

注意，这个定律所涉及到的物理量都是纯数。

 

绝对黑体的辐射定律。

从上面我们对基尔霍夫定律的分析可以知道，现在我们需要首先研究的是绝对黑体的单色辐出度。

显然这只有通过实验来进行。利用我们上面给出的绝对黑体的实际模型，就可以通过实际测量来得到单色辐出度，并进而测量得到单色辐出度按照波长的分布情况。

历史上所应用的实验装置是利用棱镜分解由上述绝对黑体的小孔在一定温度下所发射的辐射，不同波长的射线聚焦照射在热电偶上，得到不同波长射线的功率，从而得到单色辐出度按照波长的分布情况。

 

普朗克量子假设。

通过实验得到具体的绝对黑体的单色辐出度与波长和温度的关系后，就面临如何从一定的理论模型来解释实验数据的问题。

按照经典电磁理论的观点，这个问题完全可以通过对大量原子和分子的电磁运动进行统计计算来得到这个宏观规律，然而最终都失败了。

这样普朗克被迫引入了一个与经典电磁理论完全不同的观念：电磁能量的量子假说。

从经典电磁理论的观点来看，物质与辐射的相互作用可以看成是物质中的带电线性谐振子与周围空间的电磁场交换能量的过程。具体到能量是如何交换的，就不能通过经典电磁理论来了解，普朗克的假说就是这些谐振子与外界交换的能量，只能是按照以一个基本能量单位的整数倍的形式来进行，而不能在数值上连续地进行，相应的吸收与发射能量的谐振子本身的能量状态，也就只能离散的，而不是连续的。任意两个能量状态之间的差只能是一个基本能量单位的整数倍。那么谐振子的吸收能量与发射能量的过程就是谐振子在这些能量状态之间的跃迁。

普朗克推算出这个基本的能量单位对于谐振子来说是

e=hv

其中v为谐振子的频率，h为一个普适常数，称为普朗克常数。也就是说，谐振子的能量完全由它的频率决定，在这种情况下，h的量纲由能量与频率决定。

请同学们记住h的数值大小：

h=6.63×10^-34Js

在我们学习物理学时，尽管总是强调不要死记，但对于一些物理常数，还是希望能够记下来。你可能会说，在作题时，一般都会给出常数的值，为什么还需要记住它们呢？实际上记住重要物理常数的值，对于我们理解物理问题具有很重要的作用，特别是常数的数量级和单位，对于我们定性地分析问题具有以简御繁的功效。而初学者往往不能把握住。

 

Plank公式。

对于物质与辐射的相互作用，在经典物理的图象中，只有再加进去上面的那点假说，普朗克就得到了一个完美的黑体辐射公式：

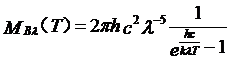
其中c为真空中的光速，k是玻耳兹曼常数。

这个公式可以推导出其他的相关经验公式，并且和实验数据很好的吻合，但它所依赖的物理图象却具有和经典物理图象根本不同的特征，那就是能量不再是连续的量，而是离散的。而这个特征是经典电磁理论所完全不能解释的。

 

光电效应。

人类几乎同时又在另一个完全不同的现象里，遭遇到了电磁场能量的量子性质，这就是光电效应。

和热辐射现象不同，在热辐射现象中，辐射与物质的相互作用表现为热能与电磁场能量的转化，光电效应里涉及到的是光能转化为电子的动能，并能形成电流。

具体的实现方式就是用紫外光或短波长的可见光照射真空中的某种金属表面，就会有电子克服金属的表面约束，从金属表面逸出，并能在电场作用下形成运流电流，即所谓光电流。

通过实验得到以下的规律：

（1）     在单位时间内，由于光的照射而释放出来的电子数目与入射光的强度成正比。

（2）     释放出来的光电子的初始动能随入射光的频率线性增加，而与入射光的强度没有关系。

（3）     对于一种特定的物质，产生光电效应的前提是入射光的频率必须大于等于一个相应的特定值，即所谓的红限，否则无论入射光的强度如何，都无法通过照射这种物质而使得它释放电子出来。

（4）     发生光电效应时，只要入射光的频率满足上面的条件，而不管它的强度如何，光照射到物质表面就马上会有电子释放出来，而没有发现有任何的迟滞现象。

仔细分析一下光电效应中所表现出来的以上规律，就会发现具有和经典电磁理论关于光的波动图象不可调和的矛盾。

（1）           根据经典的电磁波动理论，光的强度对应于光振动的振幅，也就是对应于光的能量，那么入射光作用于金属内部电子，应该是入射光能量与电子动能的转换，那么光电子的初始动能应该与入射光的强度发生关系，但实际上是与入射光的频率发生关系。

（2）           既然入射光作用于金属内部电子，是入射光能量与电子动能的转换，那么只要入射光具有足够的强度，就应该能使金属发生光电效应，但能否发生光电效应只和入射光的频率有关，而且每一种特定的物质都有它特定的能够发生光电效应的频率下限，与入射光的强度根本没有关系。

（3）           光的照射与光电子的释放之间根本没有迟滞现象，而不管入射光是否很弱；但依据经典图象，很弱的入射光应该照射一定的时间后，也就是使得传递到电子的能量应该有一定的积累过程。

所有这些基本冲突都意味着必须引入新的基本观念才能解决问题。

 

爱因斯坦方程。光子。

    爱因斯坦为了理解光电效应，从普朗克的假说，即认为热辐射与物质的相互作用过程中的能量交换是以量子的形式进行的，进一步提出涉及面更为广泛的假说：不只是在热辐射与物质的相互作用过程中的能量交换是以量子的形式进行的，根本上辐射或者说光在本性上就具有量子性或者说粒子性，也就是说，不仅在光的吸收与发射时，是表现为离散的粒子性，而且如光电效应所表现出来的那样，光在传播的过程中，也具有离散的粒子性。

光的这种粒子形态倍称为光子，每一个光子的能量就是普朗克所得到的热辐射作用里的基本能量单位hv，也就是说，光子的能量由它的频率决定，不同频率，或者说不同颜色的光子具有不同的能量。

那么光线就可以理解为以一定流量运动的光子流，光线的强度就只能理解光子流的流量的大小。这样我们再来分析光电效应，就能自恰地得到解释。

在发生光电效应的过程中，仍然是光子的能量和电子的能量的交换，只是光子的能量表示为hv，而不是用光振动的振幅来表示，而电子的能量变化包含它自身的动能和从金属表面逸出所需要作的逸出功，这就得到爱因斯坦光电效应方程：

hν=A+mV²/2

其中A为电子从金属表面逸出所需要的逸出功。

这个方程直接解释了频率在光电效应中的重要性，也自然的解释了入射光的强度与释放电子数目的关系，以及光电效应中的时间关系。

另外，这个方程还给出了通过光电效应来测量普朗克常数的途径。并给出了某种特定物质的红限的物理意义：在这个频率的光子的作用下，电子所获得的能量的大小刚好等于电子需要克服的这种金属的特定的表面逸出功的大小。

这样来理解光的本性以后，我们还可以得到光子的其他力学属性。

首先从光子的能量表达式hv，得到光子的运动质量

m_φ=ε/c²=hv/c²

而由狭义相对论的静止质量与运动质量的关系可以得到光子的静止质量为0。

然后可以得到光子的动量的表达式：

m_φc=hv/c=h/λ

这样，我们关于光的粒子性就得到了一个丰满的描述。

光电效应在检测和控制光信号时，具有重要而广泛的应用。

从此光的量子性质，或者说光的粒子图象无可置疑地确立起来了。而来自原子结构领域的研究，更加决定性地确立了量子图象的更为深刻的地位。这是下章所要讨论的。