第二十二章.原子的量子理论

研究原子结构是和研究热辐射与物质的相互作用完全不同的一个领域，在这个领域里，人们又一次独立地遭遇到了量子观念。从这里最终奠定了量子力学的基础。

 

原子光谱的实验规律。

要研究原子结构，在当时，除了放射性粒子对物质材料的轰击以外，最重要的手段就是通过原子发光现象来得到原子的光谱，从对光谱的分析得到有关原子结构的信息。

人们在收集大量的光谱资料的基础上，归纳出一些经验规律：

（1）     氢原子光谱的巴耳末系的里德伯公式。

在氢原子的光谱的可见光区，存在一系列的谱线，各根谱线的波长，或者频率，或者波数满足一定的纯粹数值上的相互关系：

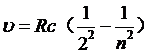
其中v为相应谱线的频率，R为里德伯常数，n取3，4，5，···时，就得到不同频率的谱线。这个公式当然也可以用波长或波数表示出来，请同学们自行练习。

（2）     碱金属光谱的一般公式。

后来发现存在一个一般的公式，就是频率由两个函数的差表示，这两个函数称为谱项，分别用正整数作为自变量：

v=T（k）-T（n），其中k小于n。

这个规律被称为里兹并合原理。

更具体的说，是如下公式：

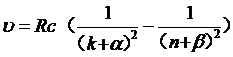
其中α与β是两个经验修正项，n决定了同一个谱系的不同谱线，而k决定了不同的谱系。

（3）    氢原子光谱的红外区域的谱线公式。

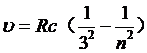 其中n=4，5，6，···

由这个公式决定的光谱线系称为帕邢系。

总结一下这些公式的共同特征就是：

（1）     谱线的频率可以用两个谱项的差计算出来；

（2）     前一个谱项的变量决定这种原子的不同谱系；

（3）     后一个谱项的变量决定这种原子在由前一个谱项所决定的谱系里的不同谱线。

注意：

这些公式在性质上完全是从已经得到的光谱数据中归纳出来的，它们只是给出某种原子的光谱中各个谱系，和每个谱系里各个谱线之间的纯粹数值关系，公式里面的所有常数都是纯粹数值，没有量纲。可以说它们是对于现象的统计规律，它只是提示我们在这么简单的公式背后肯定存在某种特别的物理机制，而它本身并没有表示任何物理上的有关原子结构的什么东西。

 

Bohr的氢原子理论。

对原子结构的研究的另一个重要途径，就是利用放射性粒子对物质进行轰击，通过测量出射粒子的力学状态的分布，来了解入射粒子在物质内部经受了哪些作用，正是物质的原子结构决定了对入射粒子的作用。由此可以反过来推导出原子的结构上的信息。

卢瑟福正是在分析α粒子散射实验的基础上，得到原子的核型结构：

原子的全部正电荷和几乎全部质量集中在原子中央的极小空间范围内，称为原子核，而原子的全部负电荷由电子携带，全部电子都围绕原子核转动。

但这个通过实验得到的最可能的结构模型，从经典电磁理论看来却是根本不能成立的。因为电子围绕圆周运动，根据经典电磁理论必然发出电磁辐射，也就是释放能量，而同时原子系统并没有从外界获得能量来维持电子的运动，这显然不能保证原子结构的基本稳定性，而我们知道，原子结构的稳定性，是我们这个世界本身存在的基本前提。

在这种尖锐矛盾的情况下，玻尔迈出了革命性的一步：既然在黑体问题与光电效应现象里，自然界已经表明电磁场的能量在本性上是具有离散的量子性质，与外部电磁场发生相互作用的原子结构本身，由于也是由电磁场相互作用决定的结构，那么原子系统内部决定电子绕核运动的电磁场能量为什么不也是具有离散的量子性质的呢？

玻尔因此提出三条有关原子结构的基本假设：

（1）           原子系统只能存在于一系列的不连续的能量状态中，每一个特定的能量状态对应于电子在特定的轨道上的绕核运动，这种运动并不释放能量，而是原子系统的一种稳定态。

（2）           电子所有可能的绕核运动的轨道必须使得电子的动量矩为h/2Π的整数倍。这就是所谓的量子化条件。

（3）           原子系统吸收或放出能量的过程，就是原子系统从一个稳定态到另一个稳定态的跃迁过程，在这个过程中所吸收或发出的单色辐射的频率由两个稳定态之间的能量差决定：

这就是频率公式。

玻尔的上述假设给出了电子运动的轨道是如何确定的，因此我们可以据此推导出氢原子的一系列物理性质，用来和其他来源的结果进行对比，就可以了解这些假设是否与事实冲突。

首先，可以计算氢原子的轨道半径。这里有几个假设：

（1）电子在核外作绕核圆周运动。

（2）向心力由电子与核之间的库仑引力提供。

（3）电子运动轨道的动量矩满足量子化条件。

这样就可以得到电子轨道半径的一般公式：

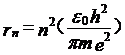
可以看到电子轨道半径与量子数的平方成正比。

而氢原子系统的能量依然可以从经典的能量图象出发，应用量子化条件来计算，这里实际上只要代入轨道半径即可：

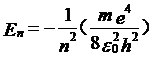
只要代入n=1，2，3，4，···就能得到氢原子系统所有可能的一系列能量状态，任何其它的能量值都是不可能氢原子系统里发现的，这种特定的分立的能量状态称为能级，而当氢原子系统在这些不同的能级之间跃迁的时候，就发出或吸收辐射，辐射光的频率由所跃迁的两个能级之间的能量差决定，实际上这就是对应于里兹并合原理里的两个谱项的差，因此由以上能量公式可以推导出里德伯公式，从而直接计算出里德伯常数，把它和实验测量所得到里德伯常数相比较，就可以知道这个理论公式相当好地与实验一致。

在理解利用公式计算能级差从而得到相应的光谱线频率时，要记住一个氢原子的一个特定的能级跃迁，只对应一条特定的光谱线，我们在氢的光谱中之所以能看多条谱线，是因为大量氢原子参与了发光，而这些氢原子并不是在进行同样的能级跃迁，而是许多不同能级之间的跃迁在这么多氢原子里，都是有可能发生的。

类似地，利用这个公式可以计算所有的谱系里所有的谱线，都一一得到了验证，并且不只是对于氢原子系统，对于似氢离子的光谱也能很好地说明，不过对于非单电子系统，就不能很好地应用了。

从上面计算氢原子结构是所设立的几个假设就可以知道，一方面仍然把电子的运动看成经典力学里的带电质点，并应用经典的轨道图象来处理电子的运动属性，另一方面又引入与经典理论完全不相容的量子化条件，使得这种处理方式具有内在的缺陷，因而受到很大的局限性。

但这个的成功还是表明了玻尔的氢原子结构理论，尽管似乎是相当人为的生硬构造，实际上在一定程度上反映了自然界内在的深刻规律，而这只是在完成量子力学以后才完全揭示出来。

 

实物粒子的波粒二象性。

历史在这里出现了极其戏剧化的场景：一方面对于在经典物理学里认为是波的光或电磁辐射，越来越显示出具有粒子的属性；另一方面对于在经典物理学里认为是粒子的对象，如电子，原子等，开始有人认为也具有波的属性，这就是德布罗意所提出的德布罗意波。

首先德布罗意是作为一个假说提出的，他认为在光的量子性里，一方面属于描述波的物理量：频率，波长，另一方面是描述粒子的物理量：能量，动量，这两方面的对应应该可以推广到一切的实物粒子上，也就是说：

p=h/λ和

E=hυ

是对一切实物粒子都适用的。

这个假说很快就得到了实验的证实，首先是电子的衍射实验，即戴维孙-革末实验。

这个实验应用和X射线的衍射实验类似的方法，只是代替X射线的是从热阴极发射出来的电子束，以一定角度投射到晶体表面，然后检测反射出来的电子反射角，利用已知晶面间距的晶体，根据布拉格公式，就可以得到电子的波长，然后再根据德布罗意的假说计算出电子的波长，两个结果相比较，验证了德布罗意的假说的合理性。

毕竟德布罗意只是提出了一种波动描述的可能性，而并没有回答究竟如何理解实物粒子的波动表象的问题，最终是玻恩给出了粒子波动性的统计解释：

粒子具有德布罗意物质波的表现，并不是意味存在某个实在的物理量的波动，而是表示粒子在空间分布具有几率性。表现粒子的波动性质的各种实验里得到波动图象只是表示粒子在空间分布的几率。

玻恩的对于粒子波动性质的统计解释最终解决了我们应该如何理解所谓波粒二象性的问题。

 

测不准关系。

微观粒子的波粒二象性，导致了我们对微观粒子的力学描述，必然会出现和经典力学里完全不同的状况。

在经典力学里，我们要知道一个质点的运动状态，首先就是要测量它的位置和动量，而对于微观粒子，测量了一个粒子的位置，然后还想测量这个粒子在这个位置的动量，就必然得不到精确值了。对于一个粒子我们同时测量它的位置和动量，所能得到的精确程度必须满足以下条件：

这就是海森堡测不准关系。

海森堡测不准关系是量子现象里的基本属性，是无法克服的。

 

波函数。Schrodinger方程。

那么要描述一个微观粒子，就不能通过给出它的位置，速度，动量一类的物理量来得到，而只能给出一种几率描述，即对于某个粒子我们在空间的某个位置测量到它存在的几率是多少。这是通过所谓波函数给出的。

这个波函数来自对粒子的波动表现的波动描述，即考虑一个自由粒子，由于它的波动表现，用一个单频平面波的波动方程来描述，然后按照德布罗意物质波的理解，用粒子的动量和能量代替波动方程里的频率和波长，就得到了描述这个微观粒子的波函数：

我们知道在应用这个方程来描述波动现象时，表示波动强度，但在用于描述粒子时，表示的是粒子在空间分布的几率密度。也就是说，乘一个体积元，得到的是在这个体积元里找到这个粒子的几率。那么在全空间里积分，得到的粒子存在几率就应该是1，这就是所谓波函数的归一化条件：

获得对于微观粒子的力学描述以后，就可以建立对于微观粒子的运动的一般运动方程。这就是所谓薛定谔方程：

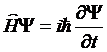
这是最一般的薛定谔方程，其中为哈密顿算符。

一般的从一个粒子的质量与这个粒子的势能函数，就可以得到这个方程，然后再根据给定的初值条件和边值条件，就可以解出我们需要的描述粒子运动状态的波函数来，然后波函数的绝对值平方就给出了粒子在一定时空位置的分布几率，这就是我们所能得到的关于粒子的最详尽的运动状态信息。

 

一维势阱。

下面我们应用定态薛定谔方程来讨论一维无穷深方势阱。

设粒子在一个有限的一维区间（-a，a）运动，在这个区间内，粒子的势能为0，在这个区间外，粒子的势能为无穷大。由此可以得到势能函数和边条件：

上述条件代入一维空间运动的粒子的定态薛定谔方程，就得到了一维无穷深方势阱的定态薛定谔方程

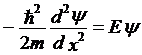
可以得到通解

其中k，A，B 是根据边条件和波函数归一化条件来确定的常数。

从而得到粒子在一维无穷深方势阱中的能量本征值为：

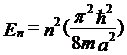，其中n=1，2，3，···

这表明粒子的能量只能取一系列的离散值，即粒子的能量是量子化的。每一个能量值称为一个能级。N为1时的能级称为基态能级。

而两个相邻能级的差为

，

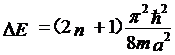可以看出，这个能量差与势阱宽度的平方成反比，也就是说，势阱宽度越小，量子化现象越明显，反过来则不明显。

最后可以解出满足相应本征值，并且经过归一化的本征函数：

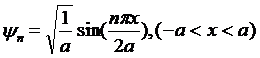
可以看出，在一维无穷深方势阱里，粒子只能在势能为0的区域运动，这种定态称为束缚定态，定态方程的解只能取驻波的形式，波节在区域边界处，而经典理论得到的结果是均匀分布。束缚定态的能级的高低是由驻波的波数来绝对的，波数越多能级越高。

 

氢原子的量子力学处理方法。

把氢原子考虑为一个电子围绕相对静止的核运动。电子的势能函数为：

得到薛定谔方程为：

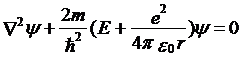
求解可以得到：

（1）     能量是量子化的，

，n=1，2，3，···

其中n称为主量子数。

（2）     轨道的动量矩是量子化的，

  ，其中l=0，1，2，3，···

l称为副量子数或角量子数。

（3）     轨道动量矩是空间量子化的，

，其中m_l=0，···称为磁量子数。

最后还有一个描述电子状态的量子数，就是自旋磁量子数，这个量子数来源于电子的自旋，不过电子的自旋不能由薛定谔方程得到。

总结起来，氢原子的核外电子的状态必须由四个量子数来描述，这就是主量子数n，决定了电子在原子里的能量；副量子数l，决定了电子围绕核运动的动量矩；磁量子数m_l，决定了电子围绕核运动的动量矩的空间取向；自旋磁量子数m_s，决定了电子自旋的动量矩的空间取向。