第四章.振动基础

之所以把振动这种运动形式，从前面的力学里单独列出来加以讨论，是因为振动具有超出力学范围的，贯穿整个物理学的一种运动的数量形式，因此在本章的学习中，我们固然要从力学的角度来分析振动的各种特征，更要对于它的一般数量形式予以特别的注意。也就是说，我们既要从具体的力学系统的角度来掌握其中的运动特征，又要站在一般的数量模型的角度来理解振动的具体力学实现。

 

    振动的一般概念。

从直观上看，振动系统的第一个要素是：系统内部具有和位置有关的作用力，因为振动物体的位置变化是围绕一个平衡位置而进行的。这就是说，系统内部必须有一个势场的作用力，而无论这个势场是什么来源。

振动系统的第二个要素是：这个系统的内部势场必须具有一个极小值位置，即所谓平衡位置。

从形式上来看，一个振动周期首先具有表征其振动强度大小的特征量，这就是振幅的概念。

然后是这个振动周期所经历的时间，即所谓周期的概念，与此相关的另一种表达方法是频率的概念，也就是一个单位时间内振动周期的个数。

对于一个确定的振动过程来说，有了上面两个特征量，还只是描述了它的全局性质，还缺乏振动的局部性质的描述，或者说初始条件的描述，也就是说，我们还无法知道在某一个时刻，系统处于振动周期的哪一个位置？这就需要有相位的概念。

至此，我们就有了完备描述振动的三个特征物理量。

 

    简谐振动。

首先我们讨论一种特定形式的振动，即振动物体所受的回复力与物体偏离平衡位置的位移成正比，并且方向总是相反。就是说：

F=-ks

其中F为回复力，s为物体偏离平衡位置的位移，k为比例系数。注意其中的负号，表示回复力总是与位移的方向相反。

这是一种最简单的振动形式，我们可以直接从上面的动力学方程得到它的运动学方程，这就是：

我们把这种可以由时间的正弦函数或余弦函数来描述的运动形式称为简谐振动。

从简谐振动的运动方程，我们可以得到几个描述振动过程的物理量。

在上面的运动方程中，A表示质点离开平衡位置的最大位移，称为振幅，T称为运动的周期，实际上也就是这个方程的函数的周期，即一个振动周期所花费的时间。

与周期相关的几个概念是圆频率和频率，频率υ定义为单位时间内振动周期的数目，圆频率ω定义为2π个单位时间内振动周期的数目。

这样简谐振动的运动方程就可以写成

其中角度量决定了质点在任一时刻的运动状态，是一个相当重要的特征物理量，因此把它定义为简谐振动的位相，而θ表示t=0，也就是质点的初始时刻的位相。

简谐振动最简单的例子就是遵从胡克定律的弹簧振子的运动，和小振幅的单摆的运动。

简谐振动实际上和圆周运动有深刻的联系，因为我们知道作圆周运动的粒子在某一方向的轴上的投影就是可以用正弦函数或余弦函数来描述的。

如图所示，用时间的正弦函数或余弦函数来描述的简谐振动正是可以通过圆周运动来描述。

可以看到，一个匀速旋转的矢量就可以表示一个简谐振动。这实际上是简谐振动的一种几何描述，被称为简谐振动的矢量图表示法。

从上面的运动方程，可以直接得到简谐振动的速度和加速度的表达式，

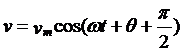
可以看到速度的位相总是比位移的位相要超前π/2，而加速度的位相总是与位移的位相相差π。也就是说作简谐振动的质点的加速度总是与它的位移成正比，而方向相反。

 

无阻尼自由振动。谐振子。

作简谐振动的力学系统称为谐振子。典型的例子就是弹簧振子。

对于弹簧振子来说，充当回复力的是遵循胡克定律的弹簧的弹力。

在我们对简谐振动的定义中，规定振子只受到一个回复力的作用，而其他的作用力的总和必须为0。也就是说，从力学的角度来看，这是一种无阻尼的自由振动。

对于无阻尼的自由振动系统，如果满足简谐振动的条件，就会存在由这个系统本身属性决定的固有周期和固有频率。

对于无阻尼的自由简谐振动系统，我们从它的运动方程就可以看出，决定它的运动状态的特征物理量并不多，圆频率是有振动系统本身的属性决定的，因此只要知道在任一时刻的振子的位移和速度，就可以完全确定这个运动的全部过程。

对于无阻尼的自由振动系统，其最主要的特征就是它是一个保守力系统，也就是说在这个系统中，只有振子的动能和某种势能（比如重力势能，弹簧势能等）之间的转换，而不涉及到别的形式的能量转换。

在后面的例题中，我们将考虑许多具体的无阻尼的自由振动。

 

阻尼振动。

相反，如果振动系统中还存在阻尼力，那么振子在运动中所受到的作用力就是回复力与阻尼力的叠加。而阻尼力总是减小回复力，因此使得振动的振幅随时间而减小。

从能量的角度来看，阻尼的发生有两种形式，一种是振动系统的能量变成热运动的能量，称为摩擦阻尼，一种是振动系统的能量变成波动形式的能量，称为辐射阻尼。

实际上无阻尼的自由振动总是一种理想运动，总是存在各种阻尼力，使得振子的能量和振幅随时间而发生衰减，而且阻尼力与振子的速度的关系往往非常复杂，我们不作具体的研究，从一般的直观上看，阻尼在使得振幅减小的同时，也使得振动的周期变长。并且如果阻尼力在一定的限度以内，则还能表现出一定的准周期性的运动，如果超出这个限度，则不再表现出任何周期性。阻尼振动的位移与时间的关系如图所示：

 

受迫振动。

我们知道实际的振动系统总是阻尼振动，那么这个系统要把振动维持下去必须从外边获得能量，也就是说有外部的力的作用。

外部作用力有两种作用形式，即单方向的力和周期作用力，我们只讨论周期作用力的情形

而一个振动系统如果受到周期性的外部驱动力，就称为受迫振动。它在运动所受到的力就是在阻尼振动的方程中再加一项周期驱动力，如果外部的周期驱动力也是按照简谐振动的规律，则得到受迫振动就会稳定为简谐振动。

 

共振。

在周期性外力作用下的受迫振动里会发生一种特别的现象，就是共振。共振的主要特点就是在外力不大的情况下，也能导致振子产生很大的振幅。正是这点使得共振具有很重要的实用价值。

共振运动最重要特征就是振幅和外力的频率有关，而且当外力频率满足一定条件时，振幅存在一个最大值，这就是说外力与振动系统发生了共振。

对于一个振动系统来说，发生共振的程度是和这个系统的品质因数相关的。

如图所示，是在不同的品质因数的情形下，振幅A作为外力频率的函数的曲线。

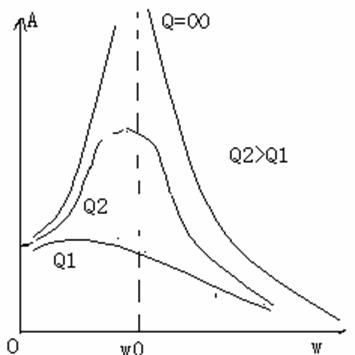
从这个图可以看到一个系统的品质因数越大，它的共振现象就越显著。

 

同方向的简谐振动的合成。

我们已经研究的简谐振动是最简单的一种形式，实际上也是最基本的一种形式，因为其他的任意形式的振动总是可以通过简谐振动的合成来得到。

这里我们能又一次体会到运动叠加性质的重要性。对于简谐振动，我们分几种简单的情况进行考虑。由于两个简谐振动要叠加，首先必须考虑它们的振动方向，所有我们分别讨论同方向与相互垂直这两种情况。

考虑了振动方向，接下来的振动特征就是频率，因此又把情况分成同频率与不同频率。

（一）相同振动方向，相同频率的振动的叠加。

我们可以用两种方式来进行研究。一种是直接根据简谐振动的运动方程表达式，通过解析式的运算来得到有明显物理意义的叠加振动的解析表达式。

设两个振动分别为：

那么直接根据运动叠加原理，可以得到合振动的表达式的形式也为：

另一种方法更为直观，就是应用上面提到的对振动的几何描述，直接对旋转矢量进行叠加，可以直观的得到合振动的表达式。

从合振动的解析表达式可以看到：

（1）两个相同方向，相同频率的振动的叠加振动保持频率不变，它的振幅和初相由两个分振动决定。

（2）两个分振动的相位相同时，合振动的振幅最大。也就是说振动加强到最大。

（3）两个分振动的相位相反时，合振动的振幅最小。也就是说振动减弱到最小。

 

（二）相同方向，频率不同的振动的叠加。

一般地说来，这时在直观上没有很直接的特征，但是当两个振动的频率很接近时，就会出现一个极为明显的现象，这就是拍的现象。

 

拍。

两个频率不同的振动方程的叠加，从解析式的角度来看，实际上就是两个正弦或余弦函数的和化为积，这样，得到的是两个简谐振动的乘积，这两个简谐振动的频率分别是两个分振动的频率的和与差。这样，我们可以想象得到合振动的图象会具有明显的周期性包络。也可以理解为一个频率很低的振动对一个频率很高的振动进行了调制。这样从现象上，我们就会看到所谓拍。

注意上面的分析，我们有意没有使用解析式推导的方式来说明，是因为我们希望强调直观思维的能力，同时也避免因繁复的数学推导而导致学习上的畏难情绪。不过，我们还是建议有兴趣的同学自己作推导，这样能更深刻的掌握振动。

 

相互垂直的简谐振动的合成。

当两个简谐振动的振动方向相互垂直时，就会在这两个相互垂直的方向所组成的平面上导致一些有趣现象的发生。

一种情况是两个振动的频率相同。这时我们会得到椭圆或圆的方程。这里我们也能进一步理解到简谐振动和圆周运动的内在深刻联系。

一种情况是两个振动的频率不同，在这两个频率为整数比时，会出现一种有趣的现象，就是所谓李萨如图形。这种图形可以通过应用示波器叠加两个适当的波动信号，而清楚地演示出来。这种特点及其应用在后面的电学里还会讨论到

 

二，疑难

 [1]。设一个单摆的最大偏角足够小，因此可以把单摆的运动看成简谐运动，如果把单摆在最大偏角处的状态取为初始状态，则单摆的初相就是。而单摆的角速度就是简谐运动的圆频率。

[答]都是错误的。

如果对于概念只是一知半解，仅仅凭借模糊的印象来答题，就会有人认为既然单摆是从最大偏角处开始运动的，是定义为单摆的初始状态，而偏角的量纲与相位的量纲一样，都是角度，那么单摆的初相自然就应该是了，这个错误想法的来源是对于简谐振动的矢量图表示法的没有正确理解。

初相之所以具有角度量纲，是因为在简谐振动的矢量图表示法里，我们取初始时刻的旋转矢量与坐标轴的夹角表示初相的大小，而与运动物体在运动中出现的任何角度没有关系。

从物理意义上来看，初相表征的是振动系统的在整个振动周期里的初始状态所处的位置，而不是属于初始状态中的某个方面的物理量，最大偏角固然属于单摆的初始状态里的一个方面的描述，但并没有代表单摆的整个初始状态在一个振动周期里的位置。因此把这个最大偏角看成初相是概念含糊所导致的错误。

在这个问题里，单摆在初始时刻处于最大位移处，也是回复力最大处，如果定义此时回复力的方向为振动的正方向，那么单摆的初相为0。

同样的，常常由于概念含糊，没有分清简谐振动的矢量图表示法与物体的简谐运动本身，因为在简谐运动的矢量图表示法中，也存在一个旋转矢量的运动，就把那个矢量运动与物体本身所作的简谐运动混淆起来，把刻画简谐振动的物理量所具有的矢量图意义与物体的简谐振动中所代表的意义混为一谈，从而出现把圆频率与角速度混为一谈的错误。

只有在旋转矢量图中的矢量旋转角速度才可以解释为振动物体的圆频率，任何其它情况下的角速度都与圆频率无关。特别是，我们知道对于单摆来说，它的圆频率是由重力加速度和摆长决定的，即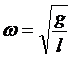，是属于单摆与地球这个系统本身的属性，与单摆的具体运动情况无关，而单摆的角速度是属于描述单摆的具体运动情况的一个物理量。

 

[2]。考虑弹簧振子系统，如果忽略弹簧的质量，则系统的固有频率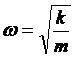。如果计入弹簧的质量，则相应的固有频率为。

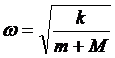[答]这是错误的。

因为弹簧的质量分布并不是在一个质点上，而可以与弹簧振子的质量加起来，构成一个等效的新弹簧振子。而弹簧的质量分布使得弹簧的对外作用力表现得更为复杂，再也不能简单地应用胡克定律来表示弹簧对于振子的回复作用力，从而也就不能应用简谐振动的频率公式。