第五章.波动基础
我们研究振动系统，一方面固然是因为振动系统在物理学与工程上的重要性，另一方面是因为振动所产生的波动现象具有更为重要的意义。
这首先是因为在实质上，波动是自然界最重要的一种传播能量的方式，在这种非常一般的意义上，波动现象非常广泛的存在于物理世界。这里我们首先讨论具体的机械振动产生的波动现象，并以此为例来研究一般的波动过程的物理图象。
机械波的产生与传播。
我们知道机械振动系统如果是一个保守系统而且与外界没有相互作用力的话，那么这个系统的能量就是守恒的，并且与外界没有能量的交换。
但一旦振子与外界发生作用，那么振子的能量就有可能传递给外界物质。而我们考虑的机械波就是由于外界物质的连续分布，并且外界物质的每个质点都具有振子的物理性质，从而出现的一种能量在空间传播的现象。
机械波的主要特征就在于它依赖传播媒质的接触作用。也就是说首先要求媒质具有连续分布的性质。然后要求组成媒质的每个质点都必须具有振子的物理性质，也就是说每个质点都必须在原始位置时是处于某种势场的极小值点。一旦偏离它的平衡位置，它就在势场的作用下进行振动，从而把能量传递给邻近的质点。
波动过程中涉及到几种方向，这几种方向能决定波动的主要特征。首先是波动振动的方向，然后是波动传播的方向，最简单的情形是两种，即如果振动方向和传播方向平行，那么这种波被称为纵波；如果振动方向和传播方向垂直，那么这种波被称为横波。当然，我们知道振动具有线性叠加性，波动同样应该也具有线性叠加性，这样任何其他的方向关系的波动都可以由这两种波通过叠加而得到。
波动传播的复杂程度首先和传播介质的分布有关。
如果传播介质是一维的，那么波的传播方向就只能在一条线上。
如果传播介质是高维的，那么波将从波源出发，向任意方向传播。而波动传播的方向称为波射线（或波线）。
由于波在介质中的传播是一个时间过程，那么我们就必须考虑波在空间中的分布的一些时间性的特征。
首先是相位的概念。由于波动是一种周期现象，因此在某一个时刻振子处于一个周期的什么位置是非常重要的物理特征。
然后在波的空间分布中同相位的各点组成一个几何面，称为波面（或波阵面）。波面的概念在应用波动图象来解释波动现象时是非常关键的。
波面的形状和波源与介质的分布性质是密切相关的。最简单的两种情形就是，如果是在各向同性的介质中，从点波源发出的波的波面就是同心球面，称为球面波，从平面波源发出的波的波面是平行平面，称为平面波。
波的传播速度。
有了波面的概念，就可以很自然地得到波的传播速度的描述。那就是波面沿着波射线传播的速度，称为相速，或波速。
由于机械波的波动过程实际上是介质的质点的振动运动的传递，因此可以想象波速是由介质的质点间相互作用性质决定的。最明显的例子就是声波的传播速度，是空气的属性决定了声速。
对于由不同频率混合起来的波动，在一定条件下，还会出现另一种速度的概念，所谓群速，在后面再讨论。
简谐波。
与简谐振动对应的就是简谐波，由于简谐振动只是运动状态在时间上的周期性，而简谐波则是同时在时间和空间上都具有周期性，因此对简谐波的数学描述要复杂一些。
简谐波的表达式有几种等价的不同形式：
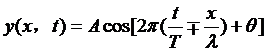
同学们一定要从数学的角度理解到这几种表达式的等价性，而在物理上则是强调了不同的描述波的性态的物理量。一定要灵活掌握，而不能被表面的形式繁复所迷惑。
下面我们就讨论这几个物理量。
波长。
从直观上讲，波长就是波动传播时在传播方向上具有相同相位的最小距离。
这里我们希望同学们能做一些扎实功夫，记忆一些日常常见的波的波长，这样能提高我们对于物理对象的直觉能力。
波的周期和频率。
一个波长范围内的波动过程可以看成我们所要研究的波动现象的一个单位。这样一个单位还有两个相关的物理量，就是周期和频率。
很显然周期就是波沿着波射线方向传播一个波长的距离所花的时间。而频率则是周期的倒数，意思就是在单位时间里波传播以一个波长为单位的数目。换句话从波源的振动的角度来说，就是单位时间内振动的次数。
对于描述波动过程的上述三个概念一定要建立非常明确的直观图象，才能在做题时不至于因为基本概念的模糊而拖延了时间。
波动方程。
迄今为止我们学习过的运动方程都是描述一个质点或刚体的，对于波动过程所涉及的对象却是连续分布的质点，并且每个质点之间并不是如刚体一样保持不变的相互位置，而是总是发生一定的变化，要找到这么一个波动过程的运动方程，我们必须注意这里所应用的物理技巧。
考虑到机械波的波动过程实际上就是介质的各个质点的相续的振动，也就是说各个质点振动过程是相同的（在介质均匀，不发生波的吸收的情况下），那么在已知波的传播速度的前提下，波动过程就可以看成是单个振动形态的匀速移动。
这样我们就可以很容易地写出波动方程来。
设在波源处（x=0）的振子的振动方程为
则在波传播到任一一点处的振动方程为
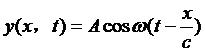
这个方程距离波源为x的某一点上在任一时刻的位移，这也就是沿着x的方向传播的平面简谐波的波动方程。
在这个方程里，波动的传播位置x和时间t是两个独立变量，这样我们可以从这个方程获得几种物理意义：
（1）如果固定t不变，那么方程描述的是介质里不同x处的波动状态的分布。
（2）如果固定x不变，那么方程描述的是介质里某一个固定位置处的振动状态，也就是那个位置的振动方程。
（3）如果这两个变量都不固定，那么这个方程描述的就是随时间而发生变化的介质里各个位置的波动状态的变化。这样就给出了一个波动过程的整体图象。
同学们在这里一定要加强对这些物理图象的直观理解，而不能只是满足于能够推导出相应的方程来就可以了。在我们解决实际问题时，这种直观理解往往能起到关键的作用。特别是在做题时，有时并不需要我们完全把解析式都列出来，有时只要具备很强的直观理解能力，就可以很快的看出答案来。这一点往往成为取得好的考试成绩的“不传之秘”。
波的能量。
我们知道波动过程传播的就是能量，那么如何计算一个波动过程所传播的能量呢？同学们一定要注意这里的物理思想。我们不妨把一个机械波的传播过程具体化为一个模型。例如一个一维的弹簧振子链，然后再具体的分析这个链的能量传播。
一般地我们得到波动过程中的能量表达式是：
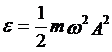
其中A为振幅，ω为频率。
从能量的角度来看波动过程，我们可以发现波动和振动的一个重要区别来。
这个区别首先在于，波动过程中的每个质点尽管也是处在振动运动的状态中，但这个振动系统并非孤立系统，而是随时在和外界作能量的交换与传递，因为如果没有这种能量的传递，也就根本不会有波动现象的发生。
这样对于介质里的每个振动中的质点而言，它总是在不断地吸收和放出能量，而它的动能和势能则发生具有相同相位的周期变化。我们知道在孤立的振子系统里，动能和势能的周期变化的相位是相反的。
能流密度。
把波的传播看成是能量的传播，就可以不妨把波动过程看成是一种能量的流动。这样一来，我们就可以进一步得到一些用来描述这种能量流动的物理量来。
首先是波的平均能流。
类似于对水流的流量度量的定义，我们把波的能流定义为单位时间内通过介质中单位面积的平均能量称为通过这一面积的平均能流（或称为在这一面积上的波的功率）。
然后是能流密度。
单位时间内通过垂直于波的传播方向的单位面积的平均能流就被称为能流密度。可见能流密度的意思就是在单位面积上的波动的功率，因此其单位一定是w·m-2。
我们有表达式：
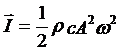
可见一定频率的波在一种确定的介质中传播时，其能流密度和波源的振幅的平方成正比。
请注意这个定义里出现了对方向的要求，也就是说能流密度是一个矢量，有时我们把它称为波的强度时，则是只取其大小，也就是说成了一个标量。
波的吸收。
当能量在介质中传播时，一般总会发生能量的耗损，因为波动所传播的能量常常会有一定比例转换为其它形式的能量，这样就表现为波在传播过程中，振幅和强度都会逐渐减小，这就是所谓波的吸收（或衰减）。
常见的波的振幅的衰减规律可以表示为：
相应的波的强度的衰减规律为：
惠更斯原理。
在波动图象中最关键的概念是波面。下面的惠更斯原理强调这个概念的重要性。
惠更斯原理：在波动过程中的任意时刻，波面上的每一个点都作为波源沿着波射线向外传递波动，而发射子波。一个波面上的所有点在任意时刻的相同相位的子波的包络面就是新的波面。
从直观上来理解惠更斯原理并不复杂，建议同学们不妨动手画一下草图，就可以得到一个很明晰的物理图象。
应用惠更斯原理我们就已经可以解释很多的波动现象，这些波动现象的共同特征就是在各向同性的均匀介质中，波动过程中保持波面的几何形状的相似性。最典型的就是下面要讨论的反射与折射，以及衍射和散射。
波的反射和折射。
这两种现象是我们非常熟悉了的，但如何基于惠更斯原理来进行理解却是要花费一些功夫的。同学们一定不要因为这两种现象本身的规律很简单，就忽略了对它的进一步理解，因为惠更斯原理是经典波动物理学的一个基本原理，我们可以通过对这样的基本现象应用这个原理来体会其一般性。而且这种理解有助于使得我们得到对于物理现象的明确图象。
波的叠加原理。
和我们在前面的质点动力学中所体会到的运动叠加原理的重要性一样，这里我们又要遇到一个具有类似重要性的叠加原理，那就是波的叠加原理。
我们在前面已经说明了波动过程，实际上就是组成介质的各个质点的振动按照一定的空间顺序和时间顺序的关联。那么两列波的叠加，归根结底也就落实到质点的振动的叠加上了， 而我们已经知道振动的叠加正是来源于一般的运动叠加原理。
因此我们显著讨论的波的叠加原理同样是来源于运动叠加原理的。只是在具体的波动现象中，我们要强调两列波的叠加并不这两列波的本来的物理性质。
波的叠加原理最直接的应用就是下面要讨论的波的干涉现象。
波的干涉
波的干涉是波动过程最典型的现象。反过来干涉现象也是关键的说明存在波动过程的判据。
首先发生干涉现象的波必须满足一定的条件，那就是
（1）必须具有相同的振动方向，
（2）具有相同的频率，
（3）而相位差必须是固定的。
很显然，两列波对同一个质点的作用的合效果是取决于这两列波的相位差的。一般的我们可以得到干涉加强与减弱的条件如下：
位相差
，k=0，1，2，3，···时，干涉加强；
位相差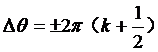
，k=0，1，2，3，···时，干涉减弱。
最好同学们能自己尝试推导一下，并且努力建立相应的直观图象，从而可以透彻的理解干涉现象的物理实质。
在一种特殊的情形下，干涉会导致所谓驻波的出现。
驻波。
驻波的产生是由振幅相等的两列相干波在同一直线上沿着相反的方向传播，从而合成为一段在空间上形状固定不动的波。这就是所谓驻波。
驻波的一个主要特点就是驻波区间内存在一些等距离的点，始终静止，称为波节。而又存在另外一些点的振幅是一列波的振幅的2倍，称为波腹。这就使得在这个区间上，波动是分段存在的。每一个分段中，各点的位相相同，而相邻分段的位相相反。各个分段相互独立振动，相邻波节之间的距离为半个波长。
波的绕射和散射。
波动在传播过程中，遇到障碍物，能够绕过障碍物的边缘，这种现象称为绕射或者衍射。这种波动的特有性质同样可以运用惠更斯原理来解释。这里的关键是障碍物使得波阵面被划分出大小可以与波长相比拟的部分，这部分的波阵面的子波的合成，就导致了衍射现象。
如果在媒质中存在尺度与波长相比拟的粒子，波动作用于这些粒子，使得这些粒子本身作为波源而发出子波，类似于被划分出来的波阵面，从而导致散射现象的发生。
声波。超声波。次声波。
频率在20Hz到20000Hz之间的机械纵波，能被人感知，称为声波。
在对声波的研究中，引入了一些特殊的概念。
声压：传播媒质中，在存在声波的传播时的压强，与不存在声波时的静压强的差，就是所传播的声波的声压。
声压本身是一种压强的波动，这种波动的振幅为
声强：即是作为机械波的声波的能流密度。因此可以得到声强的表达式为
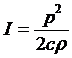
可以看出，声压与声强都随频率的增高而增高。
对于听觉而言，除了是由频率范围来决定的以外，也有一个声强范围，超过这个范围都不能被人感知为声音。
因此定义一个声强单位，以人的一个感知下限，即在1000Hz时声强为10-12Wm-2，作为测定声强的基本标准，用I0表示，则声强级定义为
I.L=10log10（I/I0）
单位为分贝（
二，疑难
1．波动方向和波的传播方向有什么区别？
答：波动方向来源于波源的振动方向，它与波的传播方向并没有必然的关系，对于纵波来说，波动方向与波的传播方向是一致的，但是对于横波来说，则是波动方向与波的传播方向相互垂直。
2．进行简谐波动的媒质的每一个体积元都是在进行简谐振动吗？
答：不对。
这是一个最容易混淆的问题。在波动过程中，媒质的体积元的动能与势能的变化是同相而且相等的，动能和势能同步地达到最大与最小，因此可以想象，每一个体积元作为一个振动系统都不是保守的能量保持守恒的系统。因为波动作为一种能量传播形式，本来就是要把能量在媒质中进行传播，而不能是媒质中的每一个体积元都保持自己的能量不发生变化。相反，简谐振动系统，则是一个保守系统，系统的机械能守恒，这样动能和势能就不能是同相的了而只能是反相的。