第八章.真实气体

从我们对理想气体的定义可以看出，我们实际上是把完全满足一个简单化的理想气体状态方程的气体定义为理想气体的。显然真实气体不可能完全满足这样的方程，因此我们必须通过实验来测量真实气体的状态变化性质，从而有可能分析与理想气体发生偏差的缘故。

 

真实气体的等温线。饱和蒸汽。临界状态。

由于很复杂的缘故，真实气体偏离了理想气体的状态变化规律，因此我们无法从关于理想气体的规律来推导出真实气体的状态变化规律，那么我们只有从实验中获得有关真实气体的状态变化的数据，通过对实验数据的分析来寻找一定的规律。

如下是二氧化碳的状态变化的压强-体积图：

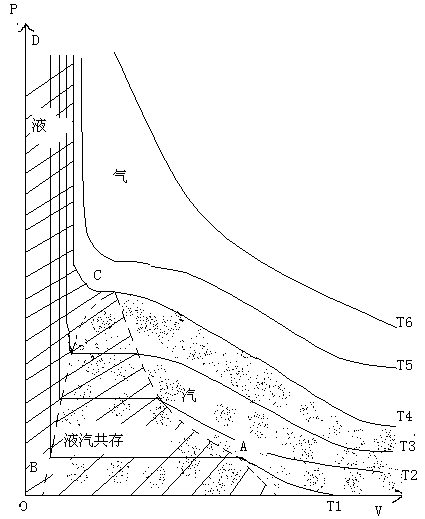
从图中可以看出：

（1）           只有在温度足够高的T₆，气体才近似于理想气体，它的等温线表现为等轴双曲线。

（2）            温度降低就会使得气体的状态变化性质偏离于理想气体，如图中的T₅。

（3）           温度降低到某个值，如图中的T₄，等温曲线上会出现一个拐点，如图中c点，这样从c点出发，再增加压强，就会使得气体液化。从而等温线上出现与压强轴平行的垂直线段。这条等温线所处的温度称为临界温度，这条等温线称为临界等温线。这个拐点称为临界点，这点的压强称为临界压强。这点的单位质量的气体的体积称为临界比容。当然在这个状态的气体称为临界状态。

（4）           再降低温度，就会在等温线上出现一段平直线，为液汽共存的状态范围，这个范围的汽体称为饱和蒸汽，相应的压强值称为饱和蒸汽压强。随着温度的降低，这个范围增大，而饱和蒸汽压强减小。

 

范德瓦耳斯方程。

对于上述真实气体的实验规律，如何加以解释，并且给出相应的气体状态方程呢？

这就需要我们对理想气体的分子运动模型加以修正，加入一些被我们忽略了的因素，显然我们不可能加入所有的因素，那就会使得状态方程极其复杂，而我们不可能从那样的方程得到好处，那么什么因素必须加以考虑，从而使得既能使得状态方程比较接近于实验数据，又能使得状态方程不是过分复杂，这就是需要洞察力的地方了，我们学习时，就必须注意这里的物理学思想，有助于提高我们在分析具体问题时的洞察力。

一种成功的修正得到所谓范德瓦耳斯方程。对理想气体作如下的修正：

（1）           不是把气体分子看成质点，而是看成具有一定的体积，这样在计算可被压缩的空间时，就必须减去气体分子本身所占有的体积。

（2）           不是把气体看成分子之间除了相互碰撞以外，不存在任何其他相互作用的系统，而是增加考虑分子之间的相互作用势，这个相互作用势的排斥力方面使得分子本身占有一定的体积，它的引力方面使得气体内部的分子之间具有内压强，从而减小了气体对外壁的压强，因此状态方程里的气体的压强必须加上内压强部分。

这样一来，我们就得到了所谓范德瓦耳斯方程：

对于1mol的气体，有状态方程如下。

。

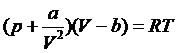其中b是1mol气体分子的等效体积，a是气体内压强与气体体积平方成反比的比例系数。与气体的性质有关。

如果在范德瓦耳斯方程中固定温度变量，就可以画出一条等温线，改变温度就可以得到一系列等温线，如下所示：

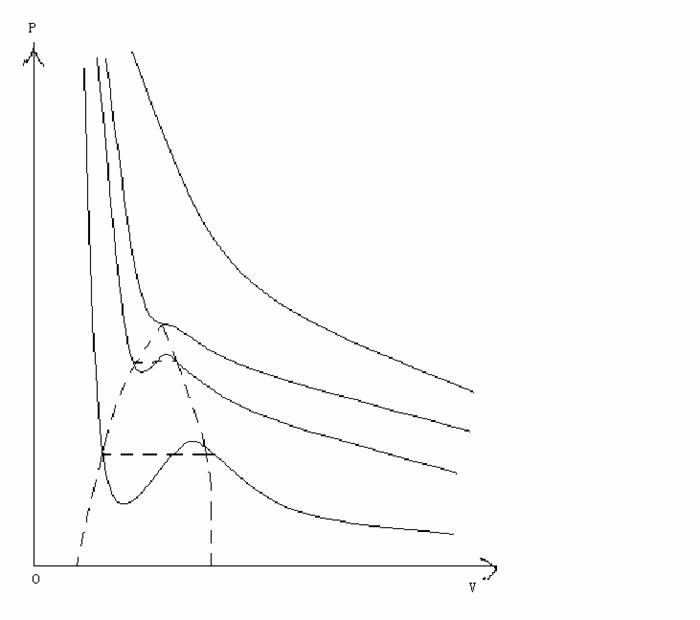
从范德瓦耳斯方程的等温线可以看出与真实气体的异同来，相同的是也能出现一条临界等温线，不同的是没有表征液汽共存的状态范围的水平直线段，在相应的区域内出现的是上凸与下凹的曲线。在一定的实验条件下，能够实现这两段曲线所表征的现象，分别得到过饱和蒸汽和过热液体。

 

焦耳-汤姆孙实验。真实气体的内能。

在绝热和保持压强不变的条件下，焦耳-汤姆孙实验通过改变气体分子的密度，观察气体温度是否变化，从而推导出气体的内能是否存在分子之间势能的部分。

实验中气体密度的变化是通过使气体从压强大的空间，经过多孔性物质迁移到压强小的空间，两个空间的压强保持不变，同时使得系统绝热，并且保持为准静态过程。

通过测量两个空间的气体的温度，测量到了温度差。这种气体通过膨胀过程而发生温度变化的现象称为焦耳-汤姆孙效应，温度降低时，称为正的焦耳-汤姆孙效应，反之温度升高时，称为负的焦耳-汤姆孙效应。

然而对于理想气体来说，由于不考虑气体分子之间的势能，所以外界作功所导致的分子内能变化就全部是动能的变化，在焦耳-汤姆孙实验的条件下，不会导致理想气体的温度变化，那么焦耳-汤姆孙实验就表明对于真实气体而言，气体内能的变化包含了气体分子之间势能的部分。也就是说，我们考虑真实气体的内能时，必须考虑到气体分子之间的势能。